Cycle Cancellation//Condorcet

[cfrank]

This is a rank-order voting system motivated by criticisms of the Condorcet criterion present here:

https://www.journals.uchicago.edu/doi/full/10.1086/682019#

A Condorcet component is a block of ballots that form a perfectly balanced Condorcet cycle. For example, a basis for 3-candidate Condorcet components is

1: A>B>C
1: B>C>A
1: C>A>B

Using the terminology in the paper, a system is said to “cancel properly” (I would rather say “cancel cycles” to avoid the moral judgment…) if the addition of any number of Condorcet components to the ballot set does not affect the result of the election. It turns out that Condorcet compliance is incompatible with cycle cancellation.

The system being considered is something along the lines as follows: first, remove all possible Condorcet components from consideration (how to address this for cycles of differing lengths?). Second, elect the Condorcet winner from the remaining ballots. This system is not Condorcet compliant because it cancels cycles.

---

For example, consider

7: A>B>C
6: B>C>A
2: C>A>B

There is no Condorcet winner here. But if we remove the Condorcet component

2: A>B>C
2: B>C>A
2: C>A>B

we are left with

5: A>B>C
4: B>C>A

There are no more Condorcet components, and the Condorcet winner of these ballots is A.

---

Correct me if I’m wrong, but I believe cycle cancellation with 3 candidates should guarantee the existence of a Condorcet winner and a Condorcet loser in the remaining ballots unless all of the ballots are canceled. This means that we can do a variant of Tideman’s IRV (Bottom Two Elimination Runoff) with triples of candidates instead of pairs: consider the 3 “worst” candidates (in a non-compensatory manner, such as fewest 1st place rankings), then cancel all 3-cycles, and eliminate the Condorcet loser. Repeat until the desired number of candidates is obtained.

[A Former User]

@cfrank I suspect you will enjoy Stable Voting

It is a recursive Condorcet method that asks "who would have won if X candidate were not in the election?" and then chooses the winner recursively based on strongest pairwise defeats. It has excellent theoretical properties, although unfortunately it's rather difficult to explain and implement.

[cfrank]

@andy-dienes I’m checking out the paper now (I’ve been doing a lot of driving so I’m mostly having my phone do text to speech lol) it’s interesting but I’ll have to actually read it.

What do you think of the concept of cancelling Condorcet cycles for 3-candidate elections?

I’m trying to think about an algebraic structure, where basically ranked ballots are associative, non-commutative products of candidates, and the ballot set is a sum of ranked ballots so that the ranked ballots form a vector space. Also, any two ranked ballots R1 and R2 have a product R1R2 that is 0 if there is some x belonging to both R1 and R2 (this guarantees that candidates don’t appear in more than one place in a ranking).

For example

abc+bca+cab

is a Condorcet component. Cancellation of cycles is the same as imposing that Condorcet components vanish, which is the same as taking the quotient of the ranked ballot vector algebra with the sub-algebra generated by Condorcet components. There seems to be a possible connection with Lie theory since saying that

abc+bca+cab=0

is known as Jacobi’s identity and is one of the structural axioms of a Lie algebra. I think reversals are also tie-inducing, since

abc+cba

also has no Condorcet winner. On the other hand it seems preferable to select b in this case by symmetry.

Forgive some jargon, I’m just trying to consider this construct mathematically. By taking the quotient with the Condorcet component algebra, we associate a ballot set with its residue modulo Condorcet cycles, and we might then have a “residual” Condorcet winner. However, even if a non-residual Condorcet winner exists, the residual Condorcet winner is not always the non-residual Condorcet winner.

This all is only pertaining so far to three candidates.

I’m trying to consider how to extend the notion of a residual Condorcet winner to four candidates. My thought is to operate by analogy with ordinary Condorcet winners, but rather than considering pairs of candidates and finding the majority winner of each pair, instead consider all triples of candidates and find the residual Condorcet winner of each triple. Basically instead of looking at the edges of the candidate graph, the triangular “faces” are looked at (which raises the complexity from quadratic to cubic in the number of candidates).

The issue with this is how to combine all of the 3-cyclic residual Condorcet winners into a single winner among 4 candidates. I wonder empirically how often the residual and non-residual Condorcet winners coincide, my guess is quite often.

[A Former User]

@cfrank

I'm skeptical that this will work out the way you want it to.

I see the idea, but the order you choose to cancel orbits in matters. For example if you have

abcdef + cdefab + efabcd + dcbafe

Should you cancel the first three terms (leaving condorcet winner = d) or the last two (leaving condorcet winner = c) ?

If you are going to try to treat a ballot set like a free algebra (modulo some cyclic relations) then now each ballot set is really an equivalence class of ballot sets. and since the condorcet winner could be different in any member of that equivalence class it's really not clear which one to choose. There is not a notion of "pre cancellation" and "post cancellation."

[cfrank]

@andy-dienes Yes indeed, I’ve been running into that breed of issue in my notes. Although I would say that the first three terms are not a Condorcet component, since you would need all six of the terms in the cyclic relation

abcdef+bcdefa+cdefab+defabc+efabcd+fabcde=0

for six candidates. For example, take four candidates and suppose we have something like

9wxyz+8wxzy+15zyxw+16zxwy

This has no 4-cyclic Condorcet components. Additionally, we can formally set each candidate to 1 and find ballots corresponding to the other three candidates. Setting w=1 we find

9xyz+8xzy+15zyx+16zxy

Again here there are no 3-cyclic Condorcet components. We have the marginal Condorcet victories

x>y, 9+8-15+16
z>y, -9+8+15+16
z>x, 9+8-15+16

and hence from the triple {x,y,z} we have the residual Condorcet winner as z.

We can do a similar computation excluding each candidate (I.e. looking at each triple). The residual Condorcet winner of {w,y,z} is z, for {w,x,z} it is also z, and of {w,x,y} it is x. These residual Condorcet winners are {x,z}. The residual Condorcet winner of these two is z, and hence z can be chosen as the winner accordingly (and happens to also be the non-residual Condorcet winner).

This I believe may be a totally well-defined system:

First, for one candidate let that candidate be the residual Condorcet winner, for two candidates let the majority winner be the residual Condorcet winner, and for three candidates take the definition already given with the addition that the residual Condorcet winner of xyz+zyx is y.

To find the residual Condorcet winner among a set of N candidates, take the N-cyclic residue of the ballots, and then from each subset of (N-1) candidates, find the corresponding residual Condorcet winner according to that N-cyclic residue. The residual Condorcet winner among the N candidates is then recursively defined to be the residual Condorcet winner among the set of residual Condorcet winners from all subsets of (N-1) candidates.

An issue comes about from the possibility that every candidate may be the residual Condorcet winner of some subset. My intuition is that by removing any N-cyclic Condorcet components, it may be impossible for every candidate to appear as one of the residual Condorcet winners. If this is the case, then we can simply iterate the procedure restricted to the set of residual Condorcet winners until a single candidate remains or a tie is reached.

I may be totally wrong about the different aspects that obstruct the existence of a Condorcet winner. Other than cycles, there are reversals, and it isn’t clear how to decide what the residual Condorcet winner of

wxyz+zyxw

should be, for example, or for any reversal of even length. This appears to be a tie between x and y.

[A Former User]

@cfrank
Anyway, I'm not sure why you would ever want to use this instead of just a method that operates on a margin graph, like e.g. the Minimax family of Condorcet methods.

Any time any ballot contains X > Y (not necessarily adjacent in the ranking), and another ballot contains Y > X, then those two will implicitly cancel each other out in the margin of defeat between X and Y. To me this seems like a strictly better approach to implement the cancellation idea.

[cfrank]

@andy-dienes I’m just trying to incorporate the points I found interesting and reasonable in the linked paper. I do find it odd that the Condorcet winner, which is defined in terms of the pairwise comparisons, firstly does not always exist (which is not that odd), and secondly can change depending on the addition or elimination of Condorcet components. This leads to the notion of a residual Condorcet winner instead, which is invariant under those alterations and has a much better chance of existing than the non-residual Condorcet winner.

I think that if the residual Condorcet winner among three candidates is defined as above, then they will almost always exist except for when the ballot set is a single perfectly balanced Condorcet cycle. Indeed I think I virtually have a proof of this as a theorem for 3 candidates, so that the residual Condorcet winner always exists for 3 candidates except in the case of a perfectly balanced tie. For this reason especially it seems to me to be a convincing canonical choice of winner, at least among three candidates.

If we handle ties for even-length reversals appropriately, it may be possible to prove by induction the universal existence at least of a weak residual Condorcet winner for any number of candidates. Possibly there’s some snag, my intuition about excluding at least one candidate may simply be false. It also isn’t totally clear even if existence is assured that the residual Condorcet winner will be a “good” winner other than in the sense of agreement on procedure, which is generally true for any voting system. I think in any case the residual Condorcet winner is at least a reasonable backup for the non-residual if not a reasonable replacement.

I’m trying to think of arguments in favor of including Condorcet components in the tally. I’m sure some argument would have to do with voter dissatisfaction or regret, and possibly stability. But I don’t see any benefit to voting dishonestly that doesn’t already exist for ordinary Condorcet methods, since in every case one would like his candidate to be a residual Condorcet winner, which is itself a Condorcet winner over a restricted subset of the ballots. I don’t see how a voter could influence which subset of the voters that “decisive” subset would be.

---

One example is given in the paper where the residual Condorcet winner is different from the ordinary Condorcet winner:

30abc+29bac+10bca+10cab+acb+cba

Here the Condorcet winner is ‘a.’ But when we eliminate Condorcet components, the residual Condorcet winner is that of

20abc+28bac

which is ‘b.’

[cfrank]

@Andy-Dienes A thought occurred to me that makes me believe the sensitivity to Condorcet components is actually not odd at all.

The thought can be best illustrated with three candidates {x,y,z}. In this case, there are two kinds of balanced Condorcet cycles, namely (xyz+yzx+zxy), and (zyx+yxz+xzy). Individually, and even combined, these Condorcet components should indicate a tie by any reasonable deliberation, since the candidates are interrelated by perfect interchangeability.

For the same reason, a ballot set that is a scalar multiple of

(xyz+yzx+zxy)+A(zyx+yxz+xzy),

where A is a non-negative real number, should equally indicate a tie.

However, consider what would occur if one of the candidates, by new information that has a negligible effect on the relationship between the other two candidates, were discovered to be an invalid winner. Without loss of generality, we can say that candidate is z. It seems reasonable to simply remove z from every ranking in the ballot set, which would transform the ballot above into

(2xy+yx)+A(2yx+xy)=(A+2)xy+(1+2A)yx

At this point, it is clear that the preferable choice between x and y, conditional on the invalidation of z, can be decided from the information available in the combination of the two oppositely oriented Condorcet components. If 1>A we should prefer x, and if A>1 we should prefer y.

In other words, combinations of Condorcet components at least provide conditional information about the preferences between candidates. If this information is considered relevant, which I think it ought to be, then ignoring Condorcet components is improper.

Informally, while Condorcet components should indicate a tie, this can be considered due to a normative balance of potential marginal dissatisfaction among the voters. If some of this dissatisfaction is actualized as a sunk cost, then the margins are changed. In a sense, this is what is being analyzed by considering the pairwise elections—the normative marginal dissatisfaction of the electorate as a whole is being minimized when the Condorcet winner exists and is chosen.

This I think upholds the concept of the Condorcet winner as a canonical choice, given that one exists.

[Lime]

2 years later

I think Saari showed in his book that Cycle Cancellation//Condorcet is equivalent to Borda!

[Toby Pereira]

I wondered about cycle removal before and posted on EM about it. I couldn't see a sensible way to make it work with more than three candidates. So it's just Borda then?

I think we probably have to just accept Condorcet methods for all their faults. I don't think a better ranked-ballot method exists that won't give horrible results in other situations. There's still approval and score-based methods to compete though.

[Toby Pereira]

@lime said in Cycle Cancellation//Condorcet:

2 years later

I think Saari showed in his book that Cycle Cancellation//Condorcet is equivalent to Borda!

I was thinking about this and I don't think Saari is right.

6: ABC
4: BCA

In this case there are only two ballot types so no cycle. A is the Condorcet winner but B is the Borda winner. In this example, B and C can be seen as clones. Borda doesn't deal well with clones, whereas cycle removal shouldn't damage independence of clones as far as I'm aware.

I'm not sure how you would do cycle removal with four or more candidates as there could be overlapping cycles, and a single pairwise comparison could be involved in more than one cycle.

One thing you could do is look at every possible triple separately (similar to how Condorcet looks at pairs separately). So within each triple you remove cycles and get the pairwise comparisons for the candidates within that. Then you could do some sort of Ranked Pairs or Rivers process to "lock in" certain triples, but it's a case of deciding how to judge which are the ones to lock in first.

It might make sense to lock in the triples that have had most cycles removed, so you're making best use of the cycle removal.

If you simply looked at defeat strength, it might be similar to Ranked Pairs or River. If e.g. A>B is the biggest defeat without any cycle removal, then there's probably at least one other candidate that you could put in a triple with A and B that doesn't create many cyclical ballots, so it's likely to remain the biggest defeat.

So provisionally I would say find the triple that has had most ballots removed, and lock in the entire order of that. Then carry on working down the list but ignoring those that create a contradiction.

[cfrank]

@toby-pereira I think our thoughts are similar in this area, I’m not sure if you were able to read the posts above and don’t blame you if not (it’s mostly me pontificating), but I’d be curious about your thoughts.

I’d started trying to work out how to address higher order cycles. At some point I came to the conclusion that it seemed virtually impossible but I don’t recall exactly why at the moment. I think it may have had something to do with the possibility of at least 2 distinct 5-cycles (think of a pentagram or the Petersen graph) and how that can lead to considering sub 4-cycles in incompatible ways, because I was trying to operate recursively. This means that for more than 4 candidates, a snag makes it difficult to find a result that would not depend in principle on the priority in which the cycles are resolved (if more than one even exists).

What is the current state of knowledge on the maximum possible number of distinct Hamiltonian cycles up to cyclic permutation in a complete directed simple graph on N vertices?

[Toby Pereira]

@cfrank I hadn't read all of it, but I've tried to go through it again just now. I haven't read the paper at the top either other than a brief skim. I've been looking at this post where you talk about a well-defined system. It obviously gets more complex when you consider cycles with more than 3 candidates, but perhaps that is the most logical way. But I wonder how much difference it would make if you just considered triples.

By the way with two ballots that are reversed (e.g. a>b>c and c>b>a) I'd see that as a tie.

[cfrank]

@toby-pereira you might find the paper interesting, if I recall it isn’t extremely long and you can get the gist without digging into the detailed examples.

I think unfortunately the system I proposed is only well-defined if there is at most one unique Hamiltonian cycle (up to cyclic permutation) in the tournament. This is probably often the case in practice but in general is simply false for more than 4 candidates, and resolving the degeneracies in a canonical way opens a can of worms. I also never finished the analysis of whether the induction for existence (almost always) of a unique residual winner actually works even in that case.

I think I abandoned it after failing to find a proof or counterexample for 4 candidates, hesitating to mess around with 5 candidates, and then realizing the degeneracy issue. I don’t remember if I found anything potentially interesting but can review my notes.

Also the only reason I wanted to settle the case of reversal ties was to extend the existence criterion which according to your notion was maybe at least half artificial.

[Toby Pereira]

@cfrank I've read the paper. Yeah, it's not too complicated, and I think I basically knew the main points it was making anyway.

By the way, as well as Condorcet with cycle removal, there is also the concept of cloneproof Borda, and it's possible that they meet in the middle somewhere. Forest Simmons came up with a method on the EM list and it is mentioned here, here and here. However, I haven't quite worked out how this method works, so if anyone can understand it better than me and put it into simple terms I would be most grateful!

[cfrank]

@toby-pereira interesting. On cursory passing his approach seems non-compensatory in terms of considering only first-place ranks and a bit arbitrary as well. But I’ll also have to examine it in more detail to have a better idea of how it works.

[Lime]

@toby-pereira said in Cycle Cancellation//Condorcet:

I was thinking about this and I don't think Saari is right.

Probably either me or whoever added this to Wikipedia misunderstanding Saari's work, rather than Saari himself.

[Lime]

@toby-pereira said in Cycle Cancellation//Condorcet:

I'm not sure how you would do cycle removal with four or more candidates as there could be overlapping cycles, and a single pairwise comparison could be involved in more than one cycle.

I think split-cycle voting tries to resolve a similar problem, by considering each simple cycle (one that starts and ends at the same point) individually/locally, then finding one winner per cycle. It might be worth looking into. Maybe you could consider each simple cycle individually and then cancel any votes?

[Lime]

@toby-pereira said in Cycle Cancellation//Condorcet:

One thing you could do is look at every possible triple separately (similar to how Condorcet looks at pairs separately). So within each triple you remove cycles and get the pairwise comparisons for the candidates within that. Then you could do some sort of Ranked Pairs or Rivers process to "lock in" certain triples, but it's a case of deciding how to judge which are the ones to lock in first.

OK, having read more about split-cycle, I think I've come to the conclusion that simple cycles (i.e. a path that starts and ends at A, without repeating any points other than A) are more likely to work than triples. An explanations of split-cycle:
Consider a simple cycle. Affirm all defeats in this cycle other than the weakest. Repeat for all possible simple cycles.

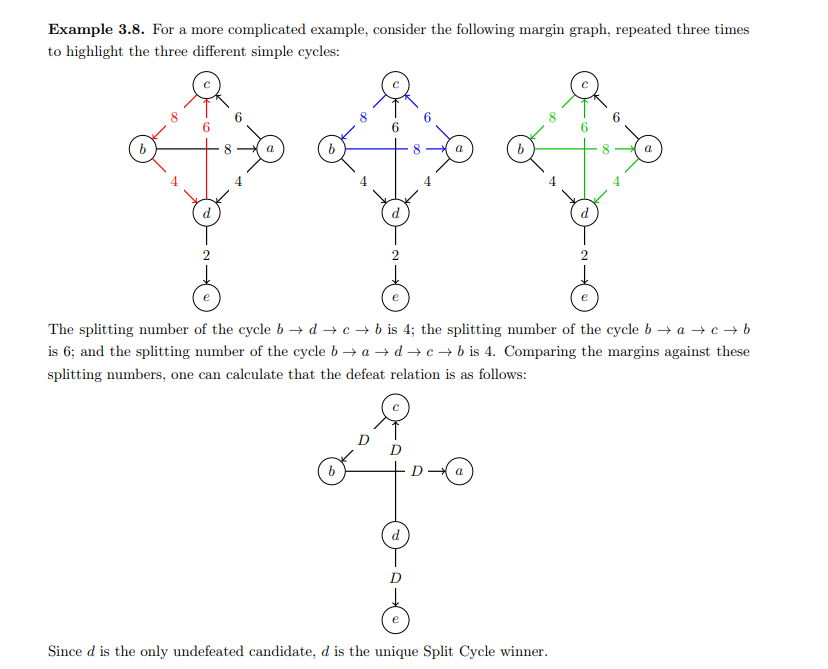
So, it's a kind of local minimax.

So you can restrict yourself to a single simple cycle at a time, and maybe consider within this group who the local winners are?

[cfrank]

@lime would you also iteratively look for the weakest edge among all simple cycles? Does this end up being different from ranked pairs? It has a kind of a co-“ranked pairs” flavor. I think the algorithm would be:

0. Set k=1.
1. If there is a Condorcet winner, elect them.
2. Identify the kth weakest edge. If it is part of a cycle, remove it. Otherwise, set k—>k+1.
3. If there are cycles remaining, repeat from (1).
4. Declare the final ranking.

It’s weird though if two edges are both the weakest and are both part of the same cycle. You could shrink all tied weakest edges in a common cycle to points and re-expand them later, effectively skipping that edge weight until the issue resolves, which would retain connectivity. That would be weird too, though.