MARS: mixed absolute and relative score
-
@casimir said in MARS: mixed absolute and relative score:
MARS voting is an attempt to find a middle way between Condorcet and utility based philosophies for single winner elections. I hoped that this balances out the strategic incentives in either group
Is there any reason you think blending Condorcet and "utility based" will help reduce strategic incentives?
I have often said that Condorcet is "median seeking," while methods like Score are "average seeking" -- albeit imperfectly for both. Median seeking implies that strength of preference is effectively ignored, which reduces the incentive to exaggerate or otherwise distort their preferences, while average seeking includes strength of preference. (I'm not a big fan of terms like "majoritarian" and "utilitarian" as they are subject to ambiguity as to what they really mean) [*]
I'd argue that if you think a particular Condorcet method is subject to strategic incentives, it is because it is not median-seeking enough. Blending it with Score-type methods would therefore tend to do the opposite.
I'll add that my gripe with most Condorcet methods is not their susceptibility to strategy, but their perceived complexity, which makes them hard to sell to the public. So I'm not against blending Condorcet with Score (that's exactly what this one does: https://www.votingtheory.org/forum/topic/130/star-like-method-reverse-star ), but I would do it to make it easier to explain and easier to vote (e.g. I prefer score-type ballots which I believe are easier to use).
* I've posted this several times, but it explains, in a simplified, 1-dimensional numerical vote, what I mean by "median seeking" and "average seeking". https://pianop.ly/voting/median.html
Note that FPTP is perfectly median seeking when there are only two candidates. The median voter in a binary-choice FPTP will always be a member of the majority.
-
@rob said in MARS: mixed absolute and relative score:
Is there any reason you think blending Condorcet and "utility based" will help reduce strategic incentives?
It was my initial intuition, that just like in STAR, the incentives to min-maxing and expressing dishonest ranking (e.g. burying) would conflict and partly cancel out.
Strategy under Condorcet involves creating or breaking a cycle. In MARS you would have to create a cycle in combined votes and score. But because score is linear it's harder to do this. And because the two metrics are correlated it's hard to burry A under B, without giving B a higher score which might allow them to beat your preferred candidate C.
So there are two cases:
-
You try to predict the outcome and pick the best strategy. This requires a good prediction and using only one strategy might not be enough to shift the result.
-
You employ both strategies and accept the higher risk that either of them backfires (or both).
Overall I think the cases where a strategy works are rarer, harder to predict and more likely to backfire. While you have more options compared to either score or Condorcet, I think in sum it's more robust against strategies.
However, I have no evidence beside reasoning. It would be great to see it tested in some VSE simulation.
Edit:
I just realized there is a simpler argument to be made. If you min-max like in score, you miss out in using preferences. If you express a dishonest order, you miss out in using scores. Either way, using one metric to vote strategically prevents you from using the other to advance your goal. A strategy is only helpful if you know that you won't need the other metric, which again is rare, hard to predict, hard to coordinate and risky. -
-
Your first example supposes that voters leave power on the table. We're not going to see that in a political election that matters.
Then again in your first example for MARS, you have 35 voters giving scores 4 4 0 when the top of the range is 5.
-
@jack-waugh said in MARS: mixed absolute and relative score:
Your first example supposes that voters leave power on the table. We're not going to see that in a political election that matters.
I would not be so quick to assume this. Voters are all kinds of irrational: look at all the voters who bullet vote in IRV even though they are strictly better off ranking more candidates.
-
Analyzing the power relations that voting systems create is enough hard work, without getting into psychology.
Moreover, US experience with FPtP indicates that voters and parties are not näive. They know to discourage people from running for office if it would spoil the chances of the lesser evil, for example. Using both extremes of the range in Range Voting a. k. a. Score Voting is even easier to understand.
-
@jack-waugh said in MARS: mixed absolute and relative score:
Analyzing the power relations that voting systems create is enough hard work, without getting into psychology.
I can mostly agree with you on that. I hate it when people try to anticipate what voters are going to attempt strategy-wise. Best to assume voters are using a "reasonable" strategy (i.e. one that actually gives them an advantage), and one with enough benefit to outweigh the extra burden of trying to come up with a workable strategy.
But bullet voting is different.... since it is simply easier. We know some number of people will do it just because they don't want to think too hard and especially, don't want to spend hours upon hours reading up on all the candidates. So unless you are going to force people to rank / rate all of them, we should at least account for bullet voting.
I don't think we should try to account for "irrational" strategies, or ones that require near superhuman ability to predict how others will vote. Those should go away over time.
As someone who has voted in a lot of ranked choice elections, I can tell you that it enough work that a lot of people will indeed bullet vote out of laziness.
-
@jack-waugh said in MARS: mixed absolute and relative score:
Your first example supposes that voters leave power on the table. We're not going to see that in a political election that matters.
Then again in your first example for MARS, you have 35 voters giving scores 4 4 0 when the top of the range is 5.
There are many voters who don't vote at all. Some intentionally because they don't like any of the alternatives. Likewise I think it's very likely that some voters will only use the lower part of the range, because they don't like any of the alternatives.
However, this method and the examples don't depend on that aspect.The same example using the full range:
voters A B C D 32 4 0 5 0 33 4 5 5 0 17 3 5 0 0 18 5 3 0 0 score 401 304 325 0 -
I think this system meets Frohnmayer balance (and is sufficiently expressive and allows the voter to weigh in on the candidates independently) and is pairwise additive, so it meets my litmus tests.
I'm not sure what tactic would be optimal in it.
-
@casimir said in MARS: mixed absolute and relative score:
Likewise I think it's very likely that some voters will only use the lower part of the range, because they don't like any of the alternatives.
I'd like to see evidence of this. I don't understand why you'd bother taking time out of your day and going to the polls, only to say "I'd like my vote to only count for 50% of what it could."
I tend to be very careful when guessing what someone is doing in their head, other than using a reasonable strategy to get the best results for themselves, or simply being lazy.
-
@rob said in MARS: mixed absolute and relative score:
I'd like to see evidence of this. I don't understand why you'd bother taking time out of your day and going to the polls, only to say "I'd like my vote to only count for 50% of what it could."
You'd be very surprised. I ran some STAR elections for a college club, and it was very very frequent that people would not normalize their scores, or they would give equal scores even when only two candidates were running for the position.
Granted, these were incredibly low-stakes elections, but I was surprised it happened at all.
-
@andy-dienes Yeah I'd tend to chalk that up to unfamiliarity with the system, more than truly being intentional. Shouldn't that tend to go away over time once a system becomes more established?
Often people go into a new system (not just voting) and behave "nicely" and naively, and when they lose, they feel resentful and say "fine, I'll play hardball too," That's my observation anyway. Behaviour tends to converge on strategic, but it can take time.
-
@rob said in MARS: mixed absolute and relative score:
Behaviour tends to converge on strategic, but it can take time.
Experience with choose-one voting supports your point.
-
Hmm, I really like this idea in theory. Have you worked out what criteria it complies with?
-
If people don't use the maximum number in Score, I'd say they are trying to support "None of the Above" (NOTA). We should require that NOTA is treated as a candidate in all elections and that the specification of the election state what shall happen in case should NOTA win. Some candidates for that are:
- new candidates sought for another attempt to elect someone to the office;
- office abolished
-
@jack-waugh said in MARS: mixed absolute and relative score:
If people don't use the maximum number in Score, I'd say they are trying to support "None of the Above" (NOTA).
I don't see how those are logically related. If we want a NOTA option, I'd think that would be a situation where every candidate gets a score of <50%, or instead we could explicitly include an option for reopening nominations.
-
@lime said in MARS: mixed absolute and relative score:
Hmm, I really like this idea in theory. Have you worked out what criteria it complies with?
I haven't looked closer into it, but because it mixes score and Condorcet, it's trivial to see that it also fails most criteria either of those fails. In the same way, it very likely satisfies criteria that are satisfied by both Condorcet and score.
I'm pretty sure it satisfies: monotonicity, independence of clones, reversal symmetry, equal vote criterion
-
The below are the result of 4,000 simulated elections following the exact conditions of the STAR paper:
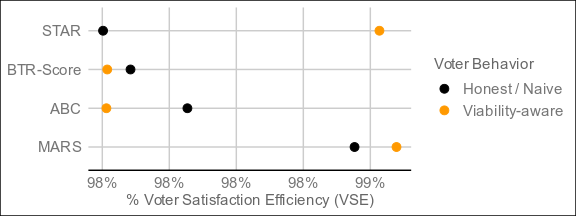
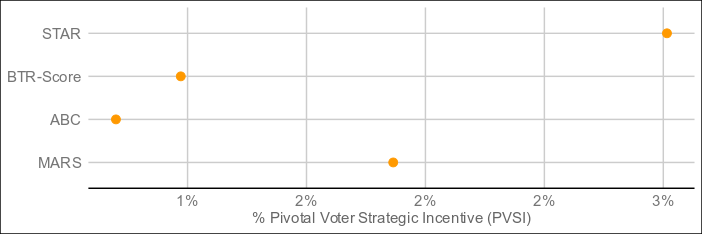
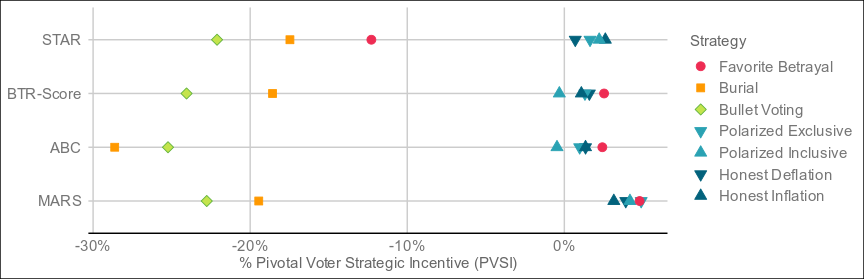
Despite the seeming complexity, MARS also resolves in around the same time as the other methods, and may quite possibly outperform methods requiring full pairwise preference matrices, which are even more complex.
-
Here's the code for use in vse-sim if interested:
@classmethod def results(cls, ballots, **kwargs): baseResults = super(MARS0to, cls).results(ballots, **kwargs) candidateIndices = list(range(len(baseResults))) remainingCandidates = candidateIndices[:] nvot = len(ballots) while len(remainingCandidates) > 1: (secondLowest, lowest) = sorted(remainingCandidates, key=lambda i: baseResults[i])[:2] voteMargin = sum(sign(ballot[lowest] - ballot[secondLowest]) for ballot in ballots)/nvot scoreMargin = (baseResults[lowest] - baseResults[secondLowest])/cls.topRank if (voteMargin > 0 and voteMargin > abs(scoreMargin)) or (scoreMargin > 0 and scoreMargin > abs(voteMargin)): remainingCandidates.remove(secondLowest) else: remainingCandidates.remove(lowest) winner = remainingCandidates[0] top = sorted(range(len(baseResults)), key=lambda i: baseResults[i])[-1] if winner != top: baseResults[winner] = baseResults[top] + 0.01 return baseResults -
I've thought of a slightly-simpler variant on MARS: Each candidate's score is equal to their range score, plus the score of the strongest (highest-scored) candidate they majority-beat. Thinking through what properties this would have.