New Simple Condorcet Method - Basically Copeland+Margins
-
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@jack-waugh I prefer cardinal methods too, but that's not what this thread is about. A viable Condorcet method is needed because "Ranked Choice Voting" has become a problem. Also I'm tired of pathetic competition -- score advocates would be forced to make better, deeper arguments if we we're going up against better ranked methods.
-
@sass Got some initial VSE results from Marcus Ogren. More people need to run some and experiment with different strategies, but they turned out pretty great. I want to get more detailed info about some of the parameters, too.
-
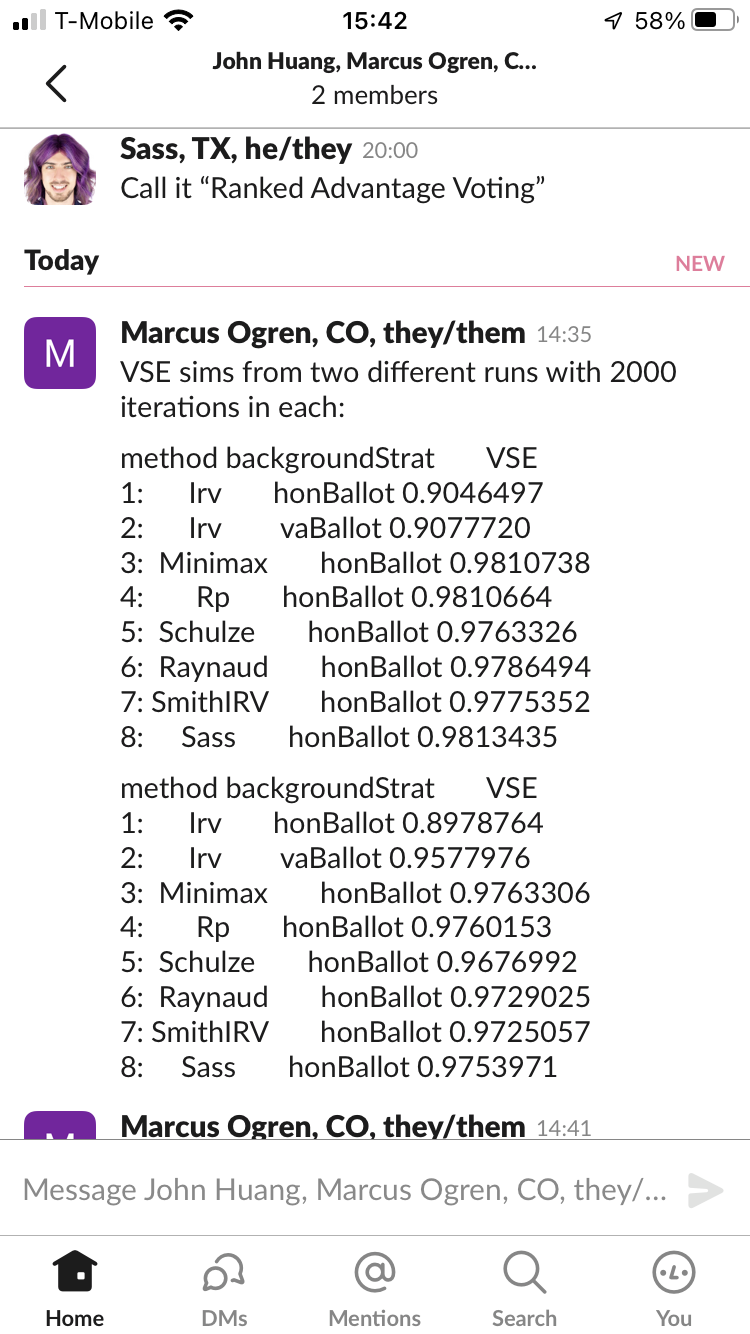
@sass said in New Simple Condorcet Method - Basically Copeland+Margins:
@jack-waugh I prefer cardinal methods too, but that's not what this thread is about. A viable Condorcet method is needed because "Ranked Choice Voting" has become a problem. Also I'm tired of pathetic competition -- score advocates would be forced to make better, deeper arguments if we we're going up against better ranked methods.
Are you saying you are still interested in promoting the method even if you can't find a case where it does better than Score?
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@jack-waugh I'm interested in getting "Ranked Choice Voting" supporters off of Instant Runoff Voting and onto a method that will help our democracy instead of actively destroying it. This could be a tool to achieve that with some of those supporters, particularly Andrew Yang.
-
What characteristics have to apply to a system for it to have a good chance of getting IRV supporters off of IRV?
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@jack-waugh For starters, the name needs to be similar. To say "Ranked Advantage Voting is also Ranked Choice Voting" seems believable and doesn't require lying. Obviously, then it needs to be a ranked method. It also needs to be easier to directly compare to Ranked Choice (Instant Runoff) Voting than score methods. Ideally, it would be sufficiently simple to explain while delivering results accurate enough to significantly improve democracy. Additionally, having it feel like a direct "upgrade" from Ranked Choice (Instant Runoff) Voting could actually lead to jurisdictions literally upgrading from Ranked Choice (Instant Runoff) Voting to Ranked Advantage Voting. Also, having it be based on voting methods that have been around longer than Ranked Choice (Instant Runoff) Voting (i.e. Condorcet) is also helpful.
"Condorcet voting has been around longer than Ranked Choice (Instant Runoff) Voting and delivers more accurate results that better address the issues of Choose-one Voting like the spoiler effect, but the trouble in the past has been describing it in a way regular voters can understand. Thanks to modern advances in voting science, we've figured out how to make Condorcet voting simpler than Ranked Choice (Instant Runoff) Voting without sacrificing Condorcet's higher level of accuracy. We call it Ranked Advantage Voting."
-
Ballot language 2.0
- Rank as many candidates as you would like.
- You are free to rank multiple candidates equally.
- Skipped ranks are simply ignored and will neither hurt nor help your vote.
<candidates and rankings>
- Candidates are compared in one-on-one matchups against every other candidate. In most elections, a single candidate will be preferred over all others, in which case that candidate is elected.
- Otherwise, all the candidates who tie for having won the most matchups become finalists; all other candidates are eliminated.
- Determine each finalist’s matchup advantage over each other finalist as the difference in the number of voters who prefer one over the other.
- Sum the matchup advantages for each finalist. The finalist with the highest total advantage is elected.
Technically, the first line in the description of the tabulation isn't necessary, but I think it will help voters feel at ease.
A simple example of matchup advantage:
If 60 voters ranked Finalist A higher than Finalist B and 40 voters ranked Finalist B higher than Finalist A, the Finalist A’s advantage over Finalist B is +20 voters and Finalist B’s advantage over Finalist A is -20 voters.
-
Is it practical to tally without computers?
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@jack-waugh Sure! It uses standard preference matrices and basic addition and subtraction. Perfectly precinct summable and hand-countable.
-
I shouldn't have asked about tallying without computers, because you are only trying here to compete against IRV. I believe computers would be required, because people would take way too long to update the preference matrix when examining a single ballot. I think no single voting system will impress both IRV supporters (however renamed it may be) and the Trump supporters who assume (with some merit) that anything that runs software can be rigged. But maybe most of the latter don't want the Americans to have democratic representation, anyway. They just pretend that is the issue when their real issue is they don't want anyone to the left of Mussolini to win.
In regard to the method overall and the power relations it would generate, if I read everything right, a comparison of this to Llull/Copeland could say that your method throws away less information in case of a cycle, in such a way that ties are less likely as the electorate grows larger.
I wonder what strategy produces better results for those who practice it than ranking according to preference would produce for them. The Gibbard theorem implies that this exists.
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@sass said in New Simple Condorcet Method - Basically Copeland+Margins:
Here's the first prototype for ballot language:
I would make the language:
- Rank as many candidates as you would like
- You may rank multiple candidates equally.
- Ranked candidates are considered better than unranked candidates.
- Skipped ranks are ignored.
Finding the winner:
- Candidates are compared in one-on-one matchups against each other.
- The candidate who wins the most matchups is elected.
- If multiple candidates tie for most wins, the tie will be broken by total margin of victory in matchups against the other tied candidates.
Reasons:
It's usually better to use fewer words for this sort of thing.
Adding the information about unranked candidates ensures that there is no ambiguity.
I don't think it's necessary to explain that Copeland's is a Condorcet method, I think it's fairly obvious from the "most wins" definition. I also don't think it is appropriate to make predictions in ballot text, such as "In most elections, a single candidate will be preferred over all others".
People know what a margin is from sports. The fewer new concepts you have to define, the better.
By framing the last step as a tiebreaker, the elimination becomes implicit.Score Sorted Margins[100]; STAR[90]; Score[81]; Approval[59]; IRV[18]; FPTP[0]
-
@jack-waugh It’s easy for poll workers who count by hand. There are three different ways to make preference matrices, so poll workers can use whichever they are most comfortable with. The most efficient procedure is to have the poll worker simply add one for each pairwise win on a ballot in the corresponding box in a matrix. This takes a bit of training, but for those with a sharp mind, it will likely be the preferred procedure. A middle approach is to list each pair of candidates and have the poll worker go through each ballot and add one to the winner between each pair, if there is one. The longest way that is probably best for recounts is to pick one pair of candidates and sort each ballot into one of three piles: one pile for the first picked candidate’s pairwise wins, the second pile for the second picked candidate’s pairwise wins, and the third pile for ballots that show no preference between the two picked candidates; then, count how many ballots are in each pile.
I would guess that a Borda strategy might work the best since the finalist margins are mathematically equivalent to tournament-style Borda. I'd love for some to run some simulations for me using that strategy.
-
I like your note on unranked candidates.
Saying "in most elections" is an appropriate prediction that I think would help to put many voter's minds at ease about understanding how the method works.
"Margin" is not well defined here, i.e. voters may think it means that a bigger difference in ranks affects the calculation. Even with the note about skipped ranks, it's important that we make it clear that the focus is simply on finalists being ranked higher or lower than each other and that the magnitude (greater than 0) of the distance between their ranks is irrelevant. My latest language is as follows:
- Rank as many candidates as you would like.
- You are free to rank multiple candidates equally.
- Skipped ranks are simply ignored and will neither hurt nor help your vote.
- Ranked candidates are considered better than candidates left unranked.
<candidates and rankings>
- Candidates are compared in one-on-one matchups against every other candidate. In most elections, a single candidate will be preferred over all others, in which case that candidate is elected.
- Otherwise, all the candidates who tie for having won the most matchups become finalists; all other candidates are eliminated.
- For each finalist, subtract the number of times they lost to each other finalist from the number of times they beat each other finalist. The finalist with the highest total difference is elected.
While I like short and concise language, I think the extra clarity (redundancy) sprinkled throughout would be helpful voters.
I only mentioned Copeland to get people on this forum to click.
-
I like the method, in general. I think Condorcet compliance is more important than most other things, and if we can make it simpler for voters to understand (both before adoption, and following a specific election) awesome.
I think your wording and explanations could use improvement, since it doesn't really come off as simple to me. I don't know if the problem is the method or just the wording and explanation, my mind is open on that.
But your general approach -- make a Condorcet compliant method marketable -- I wholeheartedly support.
Don't worry if certain people want to argue that Score is better. Score is dead in the water, in my opinion. Pro-Score arguments are fine, but I wish they weren't use to derail every other discussion.
-
@rob I'm down to keep working on ballot language. I think we need to come up with several different versions and do real field testing because every voting enthusiast seems to have a different idea about how to shift it. The shortest explanation of the tally is actually a single sentence with two clauses:
Among the candidates who tie for winning the most head-to-head matchups, elect the candidate with the best average rank.
There's some ambiguity in there in my opinion because the word "among" is being leaned on heavily, and I don't like using the mathematically equivalent "best average rank" explanation because I think it's misleading to voters despite the line saying that skipped ranks are ignored. The point is there's definitely a range of how descriptive we can be with it.
-
@sass Yes that gets to the point quickly. I like.
This seems similar in spirit to the one I was proposing recently. The main difference is that mine used cardinal ballots (intended to be identical to STAR ballots, such as if the STAR people might want to offer a Condorcet version of STAR). But otherwise it was like yours in that it ran pairwise matchups first, and if there was a tie, fell back on the simplest way to resolve it.
So your single sentence could change one word and describe mine:
Among the candidates who tie for winning the most head-to-head matchups, elect the candidate with the best average score.
https://www.votingtheory.org/forum/topic/130/star-like-method-reverse-star
That said, I think yours makes more sense for pitching it to Yang's crew, since they seem to like ranked ballots.
-
@sass said in New Simple Condorcet Method - Basically Copeland+Margins:
I would guess that a Borda strategy might work the best
W'pedia lists for Borda: "When a voter utilizes compromising, they insincerely raise the position of a second or third choice candidate over their first choice candidate, in order to help the second choice candidate to beat a candidate they like even less. When a voter utilizes burying, voters can help a more-preferred candidate by insincerely lowering the position of a less-preferred candidate on their ballot. "
If the system incents such strategies, it's no better than FPtP.
Approval-ordered Llull (letter grades) [10], Score // Llull [9], Score, STAR, Approval, other rated Condorcet [8]; equal-ranked Condorcet [4]; strictly-ranked Condorcet [3]; everything else [0].
-
@jack-waugh To me, a Borda strategy is more like filling the upper middle ranks with unknown fringe candidates. This backfires horribly when everyone does it.
I thought about it more today, though. There are five differences between my method and traditional Borda:
- The Borda calculations are performed only within the finalist set, which is extremely restrictive
- Equal ranks are allowed
- Skipped ranks are ignored
- There's no ballot completion requirement
- It uses tournament-style Borda count, which is a bit different
I think all of this combined is what allowed my method to hold up so well against Marcus' Borda strategies (which I didn't mention earlier). Regardless, the more rigorous testing, the better.
-
@jack-waugh The fact that it's only a Borda count among the tied candidates matters. It would be easier to try to cheat Copeland's directly than to cheat the Borda count at the end. Although Copeland strategy and Borda strategy do have a fair bit in common.
Score Sorted Margins[100]; STAR[90]; Score[81]; Approval[59]; IRV[18]; FPTP[0]
