Map of Voting Systems

[cfrank]

This is a rough visual conceptualization of the space of voting systems as far as my current understanding goes. I'm wondering if others consider this spectrum and the relative placement of different voting systems sensible, and if not whether there are any suggestions for changes.

Obviously the three corners of the spectrum need to be defined. I think two of them are fairly clear: stable and simple, although simple might split into "simple algorithm" and "simple ballot." The third quality I am calling "consensual," but I'm open to other titles or other delineations of the important qualities of voting systems. What I'm trying to address with consensuality is the ability to take some account of distributional justice, by avoiding highly divisive candidates and appealing to broader consensus instead of primarily to a mere majority. Another aspect might be "informed," but that doesn't really capture the notion I am trying to define.

In my opinion, the ideal system has all three qualities. Unfortunately, each one of these qualities is to a degree incompatible with the other two. My reasoning for that is as follows: as voting systems try to incorporate more information from voters to become more consensual, they open up more avenues for voters to strategize and lose stability. To combat those new avenues, they will need to become more complicated.

Here is the map I came up with, where nearness to the corresponding color is supposed to represent the relative degree of that quality found in the system:

I think voting systems that are simple are reasonably overrepresented, since voting systems that are complicated just don't have a chance at being adopted, and aren’t easy to analyze in terms of stability. I think the most complicated system in terms of its mechanism is probably IRV possibly followed by STAR. The center of the triangle is what I would consider ideal but probably unattainable.

Just as a reminder, this map is totally based on my own intuition and understanding of these systems and of voting systems in general. I would be very interested to see how others delineate the important qualities of voting systems and where they would place the systems I've included. I'm especially skeptical of where I've placed IRV and For/Against.

[rob]

@cfrank I would have put Condorcet methods way in the red (stable) corner. That's their defining characteristic, to me.

I'd describe stability in terms of the likelihood of people, after an election, thinking that if they -- and others of similar preferences and who voted similarly -- had voted differently, they could have gotten results that better met their preferences.

As for simple, Approval has simple ballots and is simple to tabulate. What isn't simple is the logic you need to use to vote with under it, at least if you want to vote with any form of strategy. But that goes back to stability and all that. (stability, vote splitting, irrelevant alternative sensitivity, strategy etc. all basically being the same issue)

[cfrank]

@rob I understand what you're saying, this map is maybe supposed to be a bit different from what it seems--a voting system way up in the stable corner is very stable but is neither simple nor consensual. I think Condorcet methods are simple and stable and somewhat consensual, which is why they are in the red/green region and close-ish to the blue region. The spectrum is supposed to capture the relative degree to which these qualities are being traded off to the extent that they are incompatible, and in terms of simplicity I'm mostly talking about comprehension of the algorithm's mechanism.

It might make more sense if "Choose-one" and "For/Against" were further down in the green region. The reason I put them in/near the stable region is that choose-one essentially locks the electorate into a strategic equilibrium, which in a sense is stable even though it's sub-optimal. Condorcet methods impose a different strategic equilibrium that is in a sense more consensual, and For/Against achieves being consensual at some intermediary, although probably it is less stable than either.

I think it would be very interesting to try to create a 2-dimensional projection of the space of voting systems based on something like the number of shared voting criteria, basically an embedding of the voting systems where distance is inversely proportional to the number of shared criteria and then flattened out into a plane or 3-d space from various angles. Something like this: https://www.youtube.com/watch?v=85XaciPBCkw

I'll have to learn more about how to use t-SNE. There are two reasons I'm interested in doing this: the first is because I personally want to see it and compare it with my own informal mental map of voting systems, and the second is because I think creating a visual representation of the space of voting systems will help newcomers navigate the arena and learn about alternative voting systems more easily. If we can make voting theory look interesting and cool to "lay" people that could accelerate public interest and further the goals of all voting theory platforms.

[rob]

@cfrank Right. It seems to me that showing it flattened is obscuring importanting things.... basically you are showing "all three" (the equivalent of white) the same as "none of the three" (the equivalent of black) as if they are the same. So you'd need something like this to show it meaningfully:

Not that I'm recommending that, but just saying.

Someone who highly values stability over everything else should be led straight to Condorcet. If you consider it also consensual and simple, awesome, but the graphic is not able to show that since the middle represents both the worst and the best.

As I've said, I think consensuality, as you describe it, arises naturally out of stable methods since they tend toward the median.

[cfrank]

@rob you're absolutely right, there needs to be a third dimension which is vertical to indicate distance from all three qualities, which perhaps should be in a cube as you depict or perhaps a tetrahedron with some indication of depth.

[cfrank]

@rob this is a topological map of several voting systems I made based on statistical similarity in terms of passing or failing 19 absolute voting system criteria; The criteria included in the analysis are as follows:

• Majority
• Majority Loser
• Mutual Majority
• Condorcet
• Condorcet Loser
• Smith
• LIIA
• IIA
• Clone-proof
• Monotonicity
• Consistency
• Participation
• Reversal symmetry
• Polynomial time
• Later No Help
• Later No Harm
• No Favorite Betrayal
• Ranks =
• Ranks >2

Here is the map, where size is supposed to indicate depth, and where distance between systems is (roughly) determined by the square root of the probability that the systems would commonly pass and fail at least N criteria, based on the relative frequencies observed among all analyzed pairs. Perhaps it should have been to the 1/3 power as a projection of a roughly 3-dimensional space, but that shouldn't change things that much and the map is at best a projection of a higher dimensional space anyway. I selected a sample of criteria to include in the map:

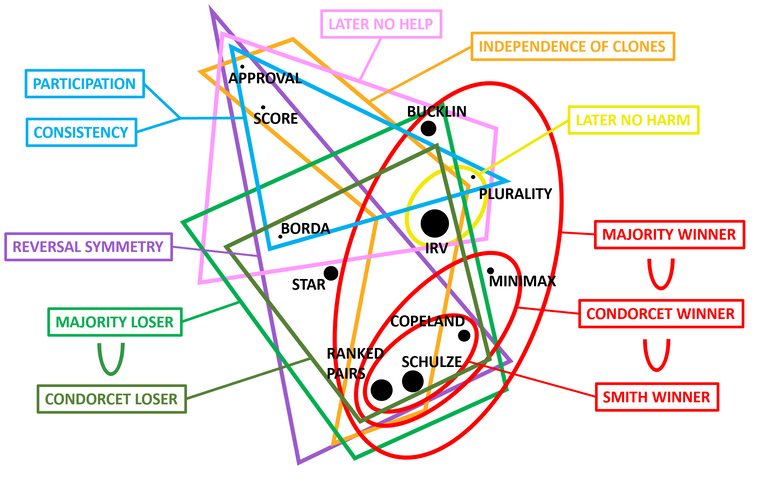
Based on commonly passing and failing absolute criteria, Schulze and Ranked Pairs are the most similar to each other, Bucklin voting is nearest to the center of the whole distribution of systems followed by STAR, and Approval voting is the most distinct from all other systems. That obviously doesn't mean that Approval will be distinct in practice, since in practice we don't care much about absolute criteria but more about propensity to conform. Regardless I though this would be an interesting and relatively easy way to map out the space of voting systems. Furthermore, everything "below" (smaller than) IRV is also monotonic.

One final thing to note is that the Majority criterion as defined here does not apply to Approval, since it is only defined for rank-order systems. An analog of it might work for Approval and that would scoot it a bit closer. Furthermore, conditioned on certain strategic equilibrium assumptions, this map changes quite a bit, since Approval becomes a Condorcet method.

[rob]

@cfrank Well, it's ummm, colorful....?

Not sure how to look at it, really. At least, I'm a bit lost as to what the spatial relationships indicate beyond the fact that certain methods are in various categories.

Was the spatial position of methods determined by a formula or did you just kind of feel them out while drawing it?

I'd love it if you came up with something that communicates to laypeople important concepts at a glance.... but I don't think this is it yet.

[cfrank]

@rob well, it had better be colorful, or else there would be no visual contrast to tell the categories apart... it isn’t going to look simple, it’s a ~19-dimensional space being compressed and projected into around 2.5 dimensions. The relative spatial positioning between systems V and W was computed as follows:

First compute the sum over all criteria of
{+1 if V and W either both pass or both fail the criterion;
{0 else.

Call this F(V,W)

Then record the relative frequency of all values of F(V,W) for each (unordered) pair (V,W). This gives a probability distribution for F(X,Y) for a pair (X,Y) chosen uniformly at random.

The distance between V and W is directly related to the relative frequency that F(X,Y) is at least as large as F(V,W). In other words, it measures how relatively dissimilar the two systems are when compared in terms of absolute criteria. Since the projection is in 2 dimensions, I took the square root of that frequency so that it would spread out reasonably in 2-d space. I had to “feel it out” to some degree, because the actual space doesn’t fit in 2 or even 3 dimensions, but the distances according to those calculations are fairly accurate.

The distance is supposed to be a measure of dissimilarity of the voting systems, relative to absolute criteria. This allows the grouping into categories to be visualized with relatively simple shapes. It's just a spatial compression of a subgraph of this table:

This kind of representation lets one quickly and systematically answer questions like, "What monotonic system is similar to IRV?" and "What Condorcet method is similar to STAR?" and “What non-Condorcet method is similar to a Condorcet method?” The answers according to this map are Bucklin and STAR, Ranked Pairs, and IRV, respectively. It also stands to reason that systems that are relatively similar across these diverse criteria are more likely to be relatively similar in other ways as well. For example, the spatial separation has naturally grouped systems with similar ballot types.

[rob]

@cfrank said in Map of Voting Systems:

"What Condorcet method is similar to STAR?"

Do I understand you to mean "similar in terms of which specific criteria they pass or fail"? If so, ok, but I don't think that actually means they are similar in particular meaningful ways.

I assume you saw that I posted that identical chart yesterday, but not as an example of what I'd consider a "good thing." Actually the exact opposite. It treats so many things as binaries when they, in order to be even remotely meaningful and useful, should be expressed as a matter of degree. It's showing them as black and white issues, rather than ones that lie on a spectrum. I can't overstate the wrongness of that approach.

For instance, Independence of Irrelevant Alternatives is all important, but -- using @robla's car analogy from that other thread -- I see it as being similar to crash-safety of a car: treating it as an all-or-nothing thing is silly. Neither of these cars can check the "perfectly safe" box, but there is a vast difference between them, which is completely ignored if you treat crash safety as a binary:

I also don't agree at all with the idea that Approval or Score pass IIA, at least not by any reasonable definition of the concept, since that conclusion relies on assumptions that might be charitably be called "unrealistic" (and a bit less charitably, "f*cking absurd" )....

Range voting, approval voting, and majority judgment satisfy the criterion if the voters grade or rate the candidates on an absolute scale that doesn't depend on who is in the running. Note that this means no voter can normalize their ballot, and so in a two-candidate election the majority can't vote strategically to make their preferred candidate win.

(from https://electowiki.org/wiki/Independence_of_irrelevant_alternatives)

So, maybe I'm misunderstanding the way you constructed your graphic, but since you posted that "compliance of selected single-winner methods" chart, and that chart really kind of represents all that I see wrong with this field of study... you got me a bit ranty.....

[cfrank]

@rob I’m not sure whether you misunderstand the way the graphic is constructed, but in any case I do generally agree with you that, individually, absolute voting theoretic criteria aren’t particularly meaningful. However, I think it’s probably mistaken to say that taking all of the criteria at once to compare voting systems is not meaningful in some way. It’s just a binary signature of the system, and even if each individual criterion only contributes some small amount of relevant information, all of them together can easily contribute a significant amount. If similar systems generally give similar signatures, and dissimilar systems generally give dissimilar signatures, it’s a reasonably proxy to allow that similarity of signatures is at least a heuristic indication that two systems are similar.

If we changed some of the categories to things like “elects the Condorcet winner at least 90% of the time when one exists” (based on some empirical data) then we would have another signature that one could argue might be more meaningful. The criteria chart was just easy to access, independent of empirical data and (mostly) independent of opinion.

To address your point about whether or not you agree with the chart on some small number of criteria, unless you disagree with more than a small handful of criteria for more than a small handful of systems, it’s generally unimportant and will not affect most of the graphic much at all.

[rob]

@cfrank said in Map of Voting Systems:

I do generally agree with you that, individually, absolute voting theoretic criteria aren’t particularly meaningful.

I'd understand your perspective better on this if you'd directly address the car crash analogy. The point is that the Wikipedia chart considers "non-zero chance of failure" to be the only metric, and that is highly misleading when it comes to real world systems where all you can do is reduce -- not eliminate -- the chance and severity of failures.

(and to take the analogy further, think of safety conscious people choosing to use a bicycle rather than a car, because someone made a list where bicycles were the only vehicle listed where you can't die in a "car accident." I think that's what people do when they arrive at Score based on it seeming to be less sensitive to irrelevant candidates than it actually is)

You said above that you wanted to "help newcomers navigate the arena and learn about alternative voting systems". If you are trying to show certain things to others that want to dive in much deeper, that's a bit different, but if you are aiming this at newcomers, I am concerned that you would be using the limited amount of time and cognitive effort they are willing (or able) to spend, only to result in sending them in the wrong direction.

[cfrank]

@rob Ok let’s do a car analogy. The criteria can be binary, such as “passes crash test A,” “passes crash test B,” “Can accelerate at this rate,” “Gets at least this gas mileage,” “Leather interior,” “No more than X miles,” “Selling for under $Y,” “Has seat warmers,” and eleven others. I think answering yes or no to all of those questions could give a pretty decent characterization of the car, it’s like 20 questions. 20 questions is very different from 1 question.

[robla]

I applaud @cfrank 's effort on the chart, even if I might disagree with the conclusions. As of right now, I don't entirely understand the chart, but that's okay. I don't entirely understand Arrow's, Gibbard's or Satterthwaite's theorem's either, and I've appreciated their effort for years.

I generally agree with @rob with respect to IIAC. I agree with him that it's absurd how cardinal-voting advocates try to declare victory and say that cardinal methods pass IIAC, and appreciate the example he provided in a different comment (@rob's comment
"For instance, if there are 3 candidates, and I approve Alice and Bob, but not Chris, for it to be independent of irrelevant candidate Chris, they have to assume that I would still approve both Alice and Bob if they were the only candidates."). In general, single-winner elections are asking voters to do one thing: pick a single winner. There is no way to avoid the comparative/competitive aspect of single-winner elections. Trying to escape the clutches of electoral impossibility theorems by saying that ratings of candidates are independent of the other candidates being considered is rank silliness (pun intended).

Generally, it seems wise not to think too hard about a specific impossibility theorem, and just assume that any good table with binary assessments of criteria are going to have "FALSE" or "NOT PASSED" or whatever for every method for at least one criterion. Election methods are graded on a curve, and each table is a different professor. Arrow's table only had four or five columns for the different criteria. Other tables have more. The tables on English Wikipedia are arbitrary and capricious (as many professors are), and seem to be rather moody with respect to pass/fail criteria. Note that when professors grade on a curve, it means that the student is in competition with other students in the class. It seems that rankings are pervasive.

Even if we agree that some tables (or some "professors") aren't very helpful, I hope we can agree that perfection is unattainable in election methods. We shouldn't spend too much time arguing about specific tables as we each try to gain personal insight on different methods. @cfrank - I suspect that your three meta-critieria ("Stable", "Simple", and "Consenual") are a bit too vague to be useful to newcomers to electoral reform. I'm not sure that there are three meta-criteria that work, but please, keep trying to find them! As we all know, it's almost impossible not to get lost in the weeds when trying to understand election methods, and a good visualization could be helpful.

[cfrank]

@robla thank you! I agree that the 3 meta-criteria are too vague, that’s a part of why I’m trying to map out the space of voting systems in a methodical way to see if any patterns emerge that might inform or conform to my vague intuitions. So far it seems like some of the obvious patterns have emerged, such as ballot type (with the possible exception of approval, which has mildly controversial inputs in the chart due to questionable assumptions).

[rob]

@cfrank said in Map of Voting Systems:

@rob Ok let’s do a car analogy. The criteria can be binary, such as “passes crash test A,” “passes crash test B,” “Can accelerate at this rate,” “Gets at least this gas mileage,” “Leather interior,” “No more than X miles,” “Selling for under $Y,” “Has seat warmers,” and eleven others. I think answering yes or no to all of those questions could give a pretty decent characterization of the car, it’s like 20 questions. 20 questions is very different from 1 question.

Well I've never seen a chart like that. NHTSA's 5-Star Safety Ratings certainly tries to distill crash safety into something more useful than a binary: https://www.nhtsa.gov/ratings
(although your mentioning multiple tests is at least better than just a single test where the only way it can pass is by a technicality such as "it isn't actually a car", which is similar to what the wikipedia chart does with giving cardinal methods a pass on IIA)

On other stuff, like "has seat warmers" or "leather interior", sure. No problem there. It would be weird, though, to try to somehow distill all those binaries down to something meaningful, rather than just putting them all out there for you to look at individually.

I would certainly not be impressed by a chart that gave binary ratings in things like "under this price point" or "gets at least this gas mileage” unless it allowed me to type in the price point or gas milage. I'd rather it just list the price and gas milage, and all the better if it allowed me to sort the list on them.

[cfrank]

@rob oh certainly, my list of criteria was totally haphazard. But even then I think answering many of those binary questions would generally lead you to the consideration of similar cars.

I don’t consider the criteria themselves to be necessarily meaningful other than being an organized collection of binary facts about the voting systems. If we used a different collection of facts, we would get a different map. It’s interesting to me to consider how or whether the map changes significantly when different chosen criteria are used. What I would want for a good characterization is for the map to be robust against reasonable changes in the criteria. In fact, showing that the important features of the map using these criteria are not robust to alterations in them is, to me, an argument against them being generally useful for characterization.

[robla]

@cfrank wrote:

some of the obvious patterns have emerged, such as ballot type

I think making the taxonomy of voting system start with "ballot type" is a mistake. Granted, a cardinal ballot can easily be converted into ranked (ordinal) ballot, but that's not the defining characteristic of an election method. It's possible to have a Condorcet-winner compliant method that uses either rated (cardinal) ballots or uses ranked ballots. Election methods should be classified by their tallying algorithm, not their user interface.

[cfrank]

@robla yes definitely, I agree. The separation here is not explicitly by ballot type, but the space of voting systems according to the way the graphic is constructed seems to be roughly split into two camps along an axis, where systems on one end of the axis seem to have cardinal/score-like ballots while those on the other end tend to have rank-order ballots. Somewhere in the middle of those for example is STAR, which has characteristics of both possibly due to the way the ballot is operated upon. Then there seem to be roughly two other dimensions (according to my rough embedding), and those dimensions in theory might somehow characterize the algorithms.

This specific map though is independent of how the systems are actually used, so the similarities being depicted will probably have a lot to do with the mathematical structure of the systems compared with the degree to which the similarities relate to how the systems operate in practice. As @rob is addressing, it would be more interesting to create a map using practical criteria based on empirical data rather than (and/or in addition to) absolute criteria.