ABC voting and BTR-Score are the single best methods by VSE I've ever seen.

[Ex dente leonem]

@casimir said:

I have to admit that I'm confused by the results. I did expect BTR-score to perform well, but I also thought that the difference to Smith//score would be to small to measure. I wonder why there is such a big difference.

I was wondering the same actually, and I think it may have something to do with how strategic voting is evaluated with Smith methods in vse-sim, specifically existing base methods run on Smith sets. For one thing the only targeted strategy available for analysis by default is bullet voting. I suggest disregarding PVSI and va behavior for Smith//Score and just looking at honest voters, which seem in line with expectations.

Also, when looking at viability-aware, STAR performs a lot better, which is also surprising. Is it that it better utilizes the score part and therefor gets the "best of both worlds"? I don't know.

My speculation is that STAR's single runoff as compared to BTR-Score's several widens the window of advantage for strategy.

How long does it take for you to run those simulations?

It depends on how many moving parts there are, but to give a rough idea here's how many minutes it takes to run 200 elections with 101 voters and 6 candidates on the following methods:

STAR - 1:38
BTR-Score: 1:49
BNR-Score - 2:51
ABC - 1:58
MARS - 1:54 (This one was a pleasant surprise)

But should be a lot faster on newer machines.

One thing to be cautious of is that these results present very small differences in a high range. It might be that the choice of model has too much of an influence to make decisive claims.

Very true, but given that these replicate as closely as possible the conditions of the STAR paper (which is cited as part of official advocacy efforts), I believe they're definitely worthy of attention. That said, these are all excellent methods VSE-wise, and I think most importantly underline how powerful sequential pairwise elimination is as part of any hybrid method,.

If it's not too much work, could you try out MARS? It's basically like BTR-score, but each round does not only compare votes, but votes+scores (both measured in % of maximum possible). Previously I thought that that would be even better than BTR-score (on the cost of being complicated), but now I'm no longer sure.

Have I got great news for you... The title of this thread is officially obsolete.

Here are the result of 4,000 elections:

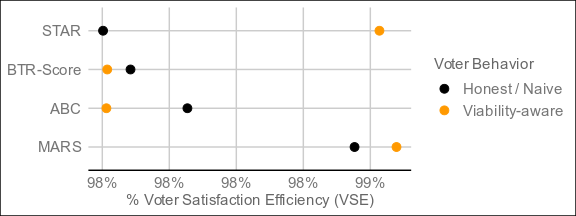
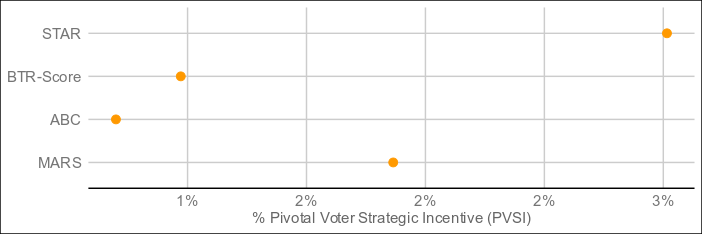
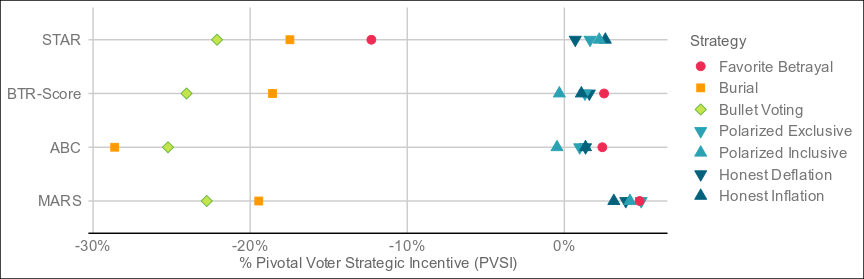
The undisputed best performer by VSE of the four is MARS, which threads the needle between Condorcet and utility methods by being neither and both, and blazing ahead as a result. The resolution mechanism is a step more complex than bottom-two runoff, but still less so than a full pairwise preference matrix (with potentially better results than such), and it resolves in around the same time as ABC and BTR-Score. For electorates who don't care too much about what's under the hood as long as it's transparent, this might be the one.

[Lime]

Thanks for these simulations, they're definitely interesting @Ex-dente-leonem

That said, I think we might be making the mistake of getting sucked deeper and deeper into a drunkard's search. The simulation results here don't really say much, except that we haven't figured out a strategy that breaks Smith//Score or ABC voting yet. That's not surprising, given we only tested 5 of them.

The difficult part of modeling voters isn't showing that one strategy or another doesn't lead to bad results. It's showing that the best possible strategy leads to good results. There's nothing wrong with testing out some strategies like in these simulations, but these are all preliminary findings and can only rule voting methods out, not in.

Just because every integer between 1 and 340 satisfies your conjecture, doesn't mean your conjecture is true. You still need to prove your conjecture.

This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

The methodology here completely fails to pick up on this, because it only tests pure strategies (i.e. no randomness and everyone plays the same strategy). In practice, pure strategies are rarely, if ever, the best. Ignoring mixed strategies has led the whole field of political science on a 15-year wild goose-chicken-chase that would've been avoided if anyone had taken Game Theory 101.

[Ex dente leonem]

@lime said:

The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

I don't believe Ranked Pairs is analyzed in the STAR paper, unless you're thinking of Jameson Quinn's original VSE document or a different paper.

I think the important takeaway here is less about trying to game out every strategy possible than the fact of how these models perform under the same conditions as what the authors believe to be their best modeled simulations, given that such simulations are an integral part of EVC's and others' advocacy efforts. (For quite necessary reasons, as we have no historical results for many methods, and as noted such historical samples would likely be unacceptably small or fail to capture the development of strategy over time.) I'd definitely welcome further testing in other simulations with mixed strategies and other voter models as realistic as we can make them.

I believe the above should be taken as impetus for theoretical analysis of why these methods seem to perform so well, and the key may be that they're all hybrid methods involving pairwise comparisons and sequential eliminations for all candidates at some point, which reasonably makes potential strategies that much harder to coordinate.

[Casimir]

@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

Have I got great news for you...

Thank you very much. That's even better than I expected.

[Kaptain5]

@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

I believe you are referring to this chart? Which shows Ranked pairs and Schulze as doing slightly better than STAR with honest voting. Does Schulze also have some failure mode which makes honest voting not the game theoretical optimal vote?

[Lime]

@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

@lime said:

The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

I don't believe Ranked Pairs is analyzed in the STAR paper, unless you're thinking of Jameson Quinn's original VSE document or a different paper.

I think the important takeaway here is less about trying to game out every strategy possible than the fact of how these models perform under the same conditions as what the authors believe to be their best modeled simulations, given that such simulations are an integral part of EVC's and others' advocacy efforts. (For quite necessary reasons, as we have no historical results for many methods, and as noted such historical samples would likely be unacceptably small or fail to capture the development of strategy over time.) I'd definitely welcome further testing in other simulations with mixed strategies and other voter models as realistic as we can make them.

I believe the above should be taken as impetus for theoretical analysis of why these methods seem to perform so well, and the key may be that they're all hybrid methods involving pairwise comparisons and sequential eliminations for all candidates at some point, which reasonably makes potential strategies that much harder to coordinate.

I'm talking about the original VSE document, yes. And my point is that I think the strategic voting assumptions are wholly unrealistic to the point that they will probably miss the vast majority of pathologies, like it does for Ranked Pairs and Schulze.

[k98kurz]

If we're going to put candidates into a tier list, we ought to include an S tier worth >1 point. I am curious about what effect that would have. Is the code used to run the ABC simulations open source?

[Ex dente leonem]

@k98kurz said:

If we're going to put candidates into a tier list, we ought to include an S tier worth >1 point. I am curious about what effect that would have.

Infinite meme potential

Is the code used to run the ABC simulations open source?

Sure, here's Jameson Quinn's vse-sim and the relevant code is:

def makeLexScaleMethod(topRank=10, steepness=1, threshold=0.5, asClass=False):
    class LexScale0to(Method):
        """
        Lexical scale voting, 0-10.
        """
        bias5 = 2.3536762480634343
        compLevels = [1,2]
        diehardLevels = [1,2, 4]

        @classmethod
        def candScore(cls,scores):
            """
            Takes the list of votes for a candidate;
            Applies sigmoid function;
            Returns the candidate's score normalized to [0,1].
            """
            scores = [1/(1+((score/cls.topRank)**(log(2, cls.threshold))-1)**cls.steepness) if score != 0 else 0 for score in scores]
            return mean(scores)
    """
    """
    LexScale0to.topRank = topRank
    LexScale0to.steepness = steepness
    LexScale0to.threshold = threshold
    if asClass:
        return LexScale0to
    return LexScale0to()

class LexScale(makeLexScaleMethod(5, exp(3), 0.5, True)):
    """
    Lexical scale voting: approval voting but retains preferences among both approved and disapproved options.
    """
    pass

to convert Score to 'Lexical Scale', and then to change STAR-style automatic runoff to sequential pairwise elimination:

def makeABCMethod(topRank=5, steepness=exp(3), threshold=0.5):
    "ABC Voting"

    LexScale0to = makeLexScaleMethod(topRank, steepness, threshold, True)

    class ABC0to(LexScale0to):

        stratTargetFor = Method.stratTarget3
        diehardLevels = [1,2,3,4]
        compLevels = [1,2,3]

        @classmethod
        def results(cls, ballots, **kwargs):
            baseResults = super(ABC0to, cls).results(ballots, **kwargs)
            candidateIndices = list(range(len(baseResults)))
            remainingCandidates = candidateIndices[:]
            while len(remainingCandidates) > 1:
                (secondLowest, lowest) = sorted(remainingCandidates, key=lambda i: baseResults[i])[:2]
                upset = sum(sign(ballot[lowest] - ballot[secondLowest]) for ballot in ballots)
                if upset > 0:
                    remainingCandidates.remove(secondLowest)
                else:
                    remainingCandidates.remove(lowest)
            winner = remainingCandidates[0]
            top = sorted(range(len(baseResults)), key=lambda i: baseResults[i])[-1]
            if winner != top:
                baseResults[winner] = baseResults[top] + 0.01
            return baseResults
    """
    """
    if topRank==5:
        ABC0to.__name__ = "ABC"
    else:
        ABC0to.__name__ = "ABC" + str(topRank)
    return ABC0to

class ABC(makeABCMethod(5)): pass

Any suggestions for improvement or optimization greatly welcome.

[Toby Pereira]

@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

Thanks for these simulations, they're definitely interesting @Ex-dente-leonem

That said, I think we might be making the mistake of getting sucked deeper and deeper into a drunkard's search. The simulation results here don't really say much, except that we haven't figured out a strategy that breaks Smith//Score or ABC voting yet. That's not surprising, given we only tested 5 of them.

The difficult part of modeling voters isn't showing that one strategy or another doesn't lead to bad results. It's showing that the best possible strategy leads to good results. There's nothing wrong with testing out some strategies like in these simulations, but these are all preliminary findings and can only rule voting methods out, not in.

Just because every integer between 1 and 340 satisfies your conjecture, doesn't mean your conjecture is true. You still need to prove your conjecture.

This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

The methodology here completely fails to pick up on this, because it only tests pure strategies (i.e. no randomness and everyone plays the same strategy). In practice, pure strategies are rarely, if ever, the best. Ignoring mixed strategies has led the whole field of political science on a 15-year wild goose-chicken-chase that would've been avoided if anyone had taken Game Theory 101.

What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters. Not under the assumption that a particular simplistic strategy model gives good results, and not even that the game theoretically optimal strategy leads to good results, but that real life voter behaviour would lead to good results.

[GregW]

@toby-pereira said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters.

To test any system in real elections we need to make the claim that the “new” system is better than the current system.

That is not a high bar, as the current system is plurality voting. IRV is also a competitor.

We may not have a firm handle on how good ABC or BTR-Score are, but we can say they are better than the choices above.

[Lime]

@toby-pereira said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters. Not under the assumption that a particular simplistic strategy model gives good results, and not even that the game theoretically optimal strategy leads to good results, but that real life voter behaviour would lead to good results.

Technically yes, but I'd feel very uncomfortable with any method where the game-theoretically optimal strategy leads to bad results, even if experiments showed the method doing well. I'd be worried voters just haven't figured out the correct strategy yet, and as soon as someone explains it to them all hell will break loose.

This is how Italy's parliament got so screwed up. They had a theoretically proportional mechanism that can be broken. It looked fine at first—because it took Berlusconi 2 or 3 election cycles to recognize the loophole and exploit the hell out of it.

So, in other words, you need an actual proof, not just "well, when I tried a couple strategies..." Otherwise, you'll find out 5-10 years later that there's some edge case where your method is a complete disaster, and after the whole IRV fiasco, electoral reform will end up completely and thoroughly discredited. (Italy went back to a mixed FPP-proportional system after the screwup.)

[GregW]

@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

I'd feel very uncomfortable with any method where the game-theoretically optimal strategy leads to bad results, even if experiments showed the method doing well. I'd be worried voters just haven't figured out the correct strategy yet, and as soon as someone explains it to them all hell will break loose.

Are you uncomfortable with BTR-Score? As a Condorcet method, it should be safer than most new systems. It would elect the “beats all” winner if there is one. Otherwise, it would elect someone from the Smith set.

As with any cardinal system, one side could decide to always bullet vote giving their favorite the highest rating and everybody else 0. The punishment would be harm to their second choices.

Would this be more, or less of a problem with BTR-Score?

Do you see another possible weakness? If so, how bad?

BTW VotersTakeCharge.us is under construction.
For a sneak peek, use the following login:
user: flywheel
Pass: squalid-fiction

[Lime]

@gregw said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

Are you uncomfortable with BTR-Score? As a Condorcet method, it should be safer than most new systems. It would elect the “beats all” winner if there is one. Otherwise, it would elect someone from the Smith set.

The problem is with strategic voters. Lots of Smith-efficient methods do really badly when voters are strategic, unfortunately, including the ones I listed (Ranked Pairs & such).

[GregW]

@lime

Perhaps testing voting systems is analogous to testing digital security, let people try to hack a new voting system. Computer simulations would be one method of hacking, creative humans, another.

Yes, real political elections are the best tests, but we have to get there from here.

[k98kurz]

@gregw there is a cyber security technique called "fuzzing" in which attacks are simulated with random data. The VSE simulations seem to provide a framework for fuzzing, where in this case the random data would be some kind of strategy. Developing a genetic algorithm to evolve a strategy that breaks a system would be an interesting side project. When I get the spare time and energy, I'll see if I can cook one up and set up a computer to just chug away at it until I have some results. (I wrote and published a library called bluegenes in case anyone wants to try stapling libraries together before I get around to it.)

[GregW]

@k98kurz said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

Developing a genetic algorithm to evolve a strategy that breaks a system would be an interesting side project. When I get the spare time and energy, I'll see if I can cook one up and set up a computer to just chug away at it until I have some results.

A great idea! To determine the best voting systems, we need to find the weaknesses of each voting system. Better testing methods are key. A tool like you propose would be invaluable.

[cfrank]

@k98kurz it’s really great you’re working on these kinds of reinforcement learning methods in this field, definitely something both very interesting and that can give us insight into how these systems work. Looking forward to hearing about any of the work in this area!

[GregW]

@cfrank said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

it’s really great you’re working on these kinds of reinforcement learning methods in this field,

Actually I do not have the mathematical expertise. If my new nonprofit, Voters Takes Charge, (under construction at voterstakecharge.us password no longer needed) receives generous support we may be able to commission such work.

[Jack Waugh]

I think I like it.

ABC || DEF

A Stein
B Williamson
C West
D Kennedy
E Harris
F Trump

[wolftune]

I wish this investigation had included BTR-RCV

(side-note: don't call it BTR-IRV, that includes "runoff" twice and is less-clear as a name)