Cycle Cancellation//Condorcet
-
2 years later

I think Saari showed in his book that Cycle Cancellation//Condorcet is equivalent to Borda!
-
I wondered about cycle removal before and posted on EM about it. I couldn't see a sensible way to make it work with more than three candidates. So it's just Borda then?
I think we probably have to just accept Condorcet methods for all their faults. I don't think a better ranked-ballot method exists that won't give horrible results in other situations. There's still approval and score-based methods to compete though.
-
@lime said in Cycle Cancellation//Condorcet:
2 years later

I think Saari showed in his book that Cycle Cancellation//Condorcet is equivalent to Borda!
I was thinking about this and I don't think Saari is right.
6: ABC
4: BCAIn this case there are only two ballot types so no cycle. A is the Condorcet winner but B is the Borda winner. In this example, B and C can be seen as clones. Borda doesn't deal well with clones, whereas cycle removal shouldn't damage independence of clones as far as I'm aware.
I'm not sure how you would do cycle removal with four or more candidates as there could be overlapping cycles, and a single pairwise comparison could be involved in more than one cycle.
One thing you could do is look at every possible triple separately (similar to how Condorcet looks at pairs separately). So within each triple you remove cycles and get the pairwise comparisons for the candidates within that. Then you could do some sort of Ranked Pairs or Rivers process to "lock in" certain triples, but it's a case of deciding how to judge which are the ones to lock in first.
It might make sense to lock in the triples that have had most cycles removed, so you're making best use of the cycle removal.
If you simply looked at defeat strength, it might be similar to Ranked Pairs or River. If e.g. A>B is the biggest defeat without any cycle removal, then there's probably at least one other candidate that you could put in a triple with A and B that doesn't create many cyclical ballots, so it's likely to remain the biggest defeat.
So provisionally I would say find the triple that has had most ballots removed, and lock in the entire order of that. Then carry on working down the list but ignoring those that create a contradiction.
-
@toby-pereira I think our thoughts are similar in this area, I’m not sure if you were able to read the posts above and don’t blame you if not (it’s mostly me pontificating), but I’d be curious about your thoughts.
I’d started trying to work out how to address higher order cycles. At some point I came to the conclusion that it seemed virtually impossible but I don’t recall exactly why at the moment. I think it may have had something to do with the possibility of at least 2 distinct 5-cycles (think of a pentagram or the Petersen graph) and how that can lead to considering sub 4-cycles in incompatible ways, because I was trying to operate recursively. This means that for more than 4 candidates, a snag makes it difficult to find a result that would not depend in principle on the priority in which the cycles are resolved (if more than one even exists).
-
@cfrank I hadn't read all of it, but I've tried to go through it again just now. I haven't read the paper at the top either other than a brief skim. I've been looking at this post where you talk about a well-defined system. It obviously gets more complex when you consider cycles with more than 3 candidates, but perhaps that is the most logical way. But I wonder how much difference it would make if you just considered triples.
By the way with two ballots that are reversed (e.g. a>b>c and c>b>a) I'd see that as a tie.
-
@toby-pereira you might find the paper interesting, if I recall it isn’t extremely long and you can get the gist without digging into the detailed examples.
I think unfortunately the system I proposed is only well-defined if there is at most one unique Hamiltonian cycle (up to cyclic permutation) in the tournament. This is probably often the case in practice but in general is simply false for more than 4 candidates, and resolving the degeneracies in a canonical way opens a can of worms. I also never finished the analysis of whether the induction for existence (almost always) of a unique residual winner actually works even in that case.
I think I abandoned it after failing to find a proof or counterexample for 4 candidates, hesitating to mess around with 5 candidates, and then realizing the degeneracy issue. I don’t remember if I found anything potentially interesting but can review my notes.
Also the only reason I wanted to settle the case of reversal ties was to extend the existence criterion which according to your notion was maybe at least half artificial.
-
@cfrank I've read the paper. Yeah, it's not too complicated, and I think I basically knew the main points it was making anyway.
By the way, as well as Condorcet with cycle removal, there is also the concept of cloneproof Borda, and it's possible that they meet in the middle somewhere. Forest Simmons came up with a method on the EM list and it is mentioned here, here and here. However, I haven't quite worked out how this method works, so if anyone can understand it better than me and put it into simple terms I would be most grateful!
-
@toby-pereira interesting. On cursory passing his approach seems non-compensatory in terms of considering only first-place ranks and a bit arbitrary as well. But I’ll also have to examine it in more detail to have a better idea of how it works.
-
@toby-pereira said in Cycle Cancellation//Condorcet:
I was thinking about this and I don't think Saari is right.
Probably either me or whoever added this to Wikipedia misunderstanding Saari's work, rather than Saari himself.

-
@toby-pereira said in Cycle Cancellation//Condorcet:
I'm not sure how you would do cycle removal with four or more candidates as there could be overlapping cycles, and a single pairwise comparison could be involved in more than one cycle.
I think split-cycle voting tries to resolve a similar problem, by considering each simple cycle (one that starts and ends at the same point) individually/locally, then finding one winner per cycle. It might be worth looking into. Maybe you could consider each simple cycle individually and then cancel any votes?
-
@toby-pereira said in Cycle Cancellation//Condorcet:
One thing you could do is look at every possible triple separately (similar to how Condorcet looks at pairs separately). So within each triple you remove cycles and get the pairwise comparisons for the candidates within that. Then you could do some sort of Ranked Pairs or Rivers process to "lock in" certain triples, but it's a case of deciding how to judge which are the ones to lock in first.
OK, having read more about split-cycle, I think I've come to the conclusion that simple cycles (i.e. a path that starts and ends at A, without repeating any points other than A) are more likely to work than triples. An explanations of split-cycle:
Consider a simple cycle. Affirm all defeats in this cycle other than the weakest. Repeat for all possible simple cycles.
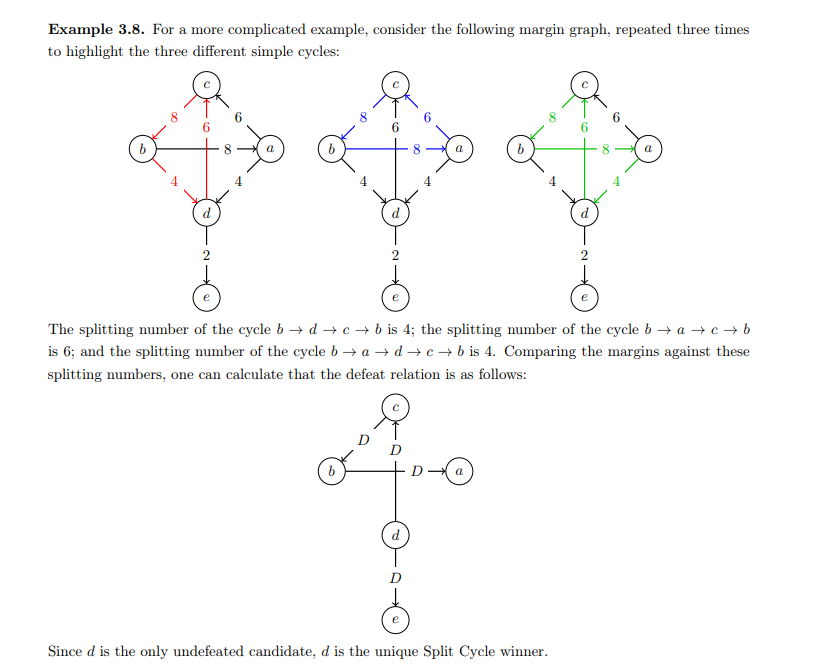
So, it's a kind of local minimax.So you can restrict yourself to a single simple cycle at a time, and maybe consider within this group who the local winners are?
-
@lime would you also iteratively look for the weakest edge among all simple cycles? Does this end up being different from ranked pairs? It has a kind of a co-“ranked pairs” flavor. I think the algorithm would be:
- Set k=1.
- If there is a Condorcet winner, elect them.
- Identify the kth weakest edge. If it is part of a cycle, remove it. Otherwise, set k—>k+1.
- If there are cycles remaining, repeat from (1).
- Declare the final ranking.
It’s weird though if two edges are both the weakest and are both part of the same cycle. You could shrink all tied weakest edges in a common cycle to points and re-expand them later, effectively skipping that edge weight until the issue resolves, which would retain connectivity. That would be weird too, though.
-
@cfrank said in Cycle Cancellation//Condorcet:
Does this end up being different from ranked pairs? It has a kind of a co-“ranked pairs” flavor.
Yes, it's slightly different. Very roughly (this isn't actually a correct characterization), you can think of it as being "all the places where Ranked Pairs, River, and Schulze agree" (all three methods return a winner selected by Split Cycle).
TBC, Split-Cycle isn't resolute (it often—and by often I mean like 1% of elections :p—returns multiple winners). So it's more of a way to winnow down the set of potential winners.
@cfrank said in Cycle Cancellation//Condorcet:
Identify the kth weakest edge. If it is part of a cycle, remove it. Otherwise, set k—>k+1.
This is different from Split-Cycle. Actually, I think it's equivalent to Minimax.
-
@lime yes they’re different. I’ll have to understand split cycle.
Still, the concept of shrinking the weakest edges in a common cycle into single nodes is interesting to me just mathematically. If the collapsed nodes are labeled as candidate subsets, you get a new marginal victory graph between over candidate subsets, and applying the same algorithm to these “meta nodes” by aggregating marginal victories between them can eliminate groups of candidates. I don’t know if that’s equivalent to any known method. It is a Condorcet method and satisfies the Condorcet loser criterion, which means it can’t be Minmax.
Smith//Minmax is also somewhat interesting. Is the following equivalent to split cycle voting?:
- If there is a Condorcet winner, elect them.
- If there is a Condorcet loser, remove them, repeating until there are no Condorcet losers.
- Of all edges that belong to cycles, identify those of minimum weight. Create a new tournament without those edges.
- Repeat step (3) on the newest tournament until no cycles remain. Then remove all candidates who are defeated (preserve only the undefeated candidates).
- Return to the original graph including only the undefeated candidates. Repeat from (1).
-
@cfrank said in Cycle Cancellation//Condorcet:
Of all edges that belong to a cycle, identify those of minimum weight. Create a new tournament without those edges.
I think this step needs to be modified slightly to preserve those edges if they're part of another simple cycle where they're not the minimum-weight edge. In other words, we only eliminate an edge if it's the minimum-weight edge in every simple cycle it's a part of. If it's the minimum-weight edge in one cycle, but a very strong edge in another cycle, you don't want to eliminate it.
-
@lime since we would be iterating through the edges that belong to cycles in order of ascending weight, any edge under consideration would automatically be the minimum weight edge of every cycle it is a part of. I think maybe it wasn't clear that equivalently, we can ask for each edge, "Is there some cycle to which this edge belongs?" If yes, it is in the search space of edges, and then we identify the edges in the search space of minimum weight.
Generally, whether an edge (u,v) belongs to a cycle can be checked by removing the edge and doing a (depth-first) search for a path from u to v, since (u,v) belongs to a cycle if and only if such a path exists.
But in any case it's just a concept, similar to Young's method and Dodgson's method, since it tries to perturb the ballot set in a conservative way until a Condorcet winner emerges.
-
Just bumping this again. Since cycle removal works quite cleanly for 3 candidates, you could have a STAR-type method where the top 3 by score go into the run-off instead of 2, and with the top 3, you then remove cycles and find the Condorcet winner.
Alternatively you might want to come up with a cloneproof measure to find the top 3, perhaps similar to the score excess method that I posted here, based on Chris Benham's approval opposition.