ABC voting and BTR-Score are the single best methods by VSE I've ever seen.

[cfrank]

@ex-dente-leonem could this be generalized with a ranking plus approval cutoff with the same runoff mechanism? I also feel like there may be burial issues, am I wrong?

[Ex dente leonem]

@cfrank I only generalized it for converting score to nonlinear score plus approval cutoff, but maybe you'll find it helpful:

(1/(1+((s/n)^(log(2)/log(t))-1)^α)

where s = score, n = top rank, t = threshold between 0 and 1, and α = steepness.

From here.

With high enough α the threshold approaches verticality and the function approximates approval. There's probably a much simpler way to do it with rounding or floor/ceiling, but the issue is how to retain preferences.

(Very preliminary testing shows that for some reason the function may be optimized for VSE around α = e, which seems in line with my (purely speculative philosophically biased lol) intuition that the best voter utility may be nonlinear and perhaps looks more like logarithmic score voting.)

As for burial, seems to be the opposite; it consistently shows the best resistance out of the methods I've tested, which to be fair have only been the above. Any burial resistance seems more due to the method itself and not necessarily the pairwise elimination, since BTR-Score is less resistant (but still performs very well).

[cfrank]

@ex-dente-leonem what I mean is that a voter could submit a ranking of candidates and then choose above which ranking they want to give approval points. Then there’s no need to use any fixed set of ordinal scores like A,B,C,etc. That gives voters more flexibility to indicate their preferences.

In any case I think it makes sense, and I like the way the method works. It seems to address a lot of issues at once.

The system I consider which is more or less the same but with a minor adjustment is for voters to submit (partial) rankings of candidates (with equality) and a rank for approval cutoff. Then the winner would be decided in accordance with the result of the following algorithm:

1. Let N be the number of candidates.
2. From the N candidates with the lowest approval ratings, determine if a Condorcet loser exists.
3. If no Condorcet loser exists, reduce N by 1 and repeat from step 2.
4. If a Condorcet loser exists, eliminate them from the election, let N be the number of remaining candidates, and repeat from step 2 until a single candidate remains.

There may be a more efficient algorithm that results in the same winner. It’s basically “bottom N runoff” where N starts large and decreases conservatively to partially mitigate the possible dependence of the end result on the order of elimination.

What else is nice is that if there are tied weak Condorcet losers, they can all be eliminated at once, and the algorithm will halt when there is a Condorcet cycle of equally approved candidates, which will almost always be just one candidate.

[Ex dente leonem]

@cfrank Like a total preference order + sequential elimination? That's a really great idea, I'll try to come up with something.

[cfrank]

@ex-dente-leonem in principle some kind of heuristics could be used to speed up that algorithm^ I wonder if it can be written in O(N logN) expected time. I would also be interested to know if this method is actually the same as Condorcet//Approval.

And if that’s true, it seems like a generalization would be (Absolute) Smith//Score as suggested by @Lime and @Jack-Waugh (and perhaps many others).

Otherwise if they’re different, it would also be interesting to see how they differ.

[Ex dente leonem]

@cfrank I couldn't come up with a way to write/convert a method for this in vse-sim, but I wanted to try out your bottom-N runoff suggestion for the BTR methods.

I literally said "Holy shit" when I did my first run of 200 just now and saw this.

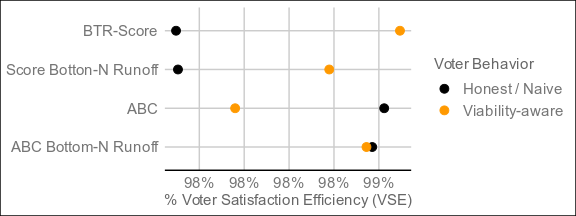
I eliminated weak Condorcet losers instead since that seemed to cause less problems with ties, and eliminated the lowest scorer at N = 1 so the algorithm wouldn't halt, but let me know if that's okay or not. I'm about to do a run of 4000 with the current settings and will post the results when complete.

[Ex dente leonem]

@cfrank Here are the results of 4,000 runs under the same conditions as the original, with STAR included for comparison:

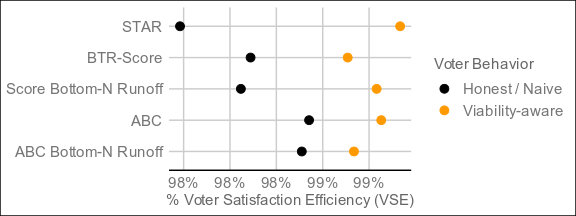
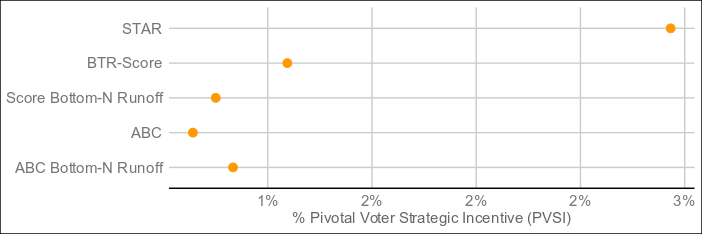
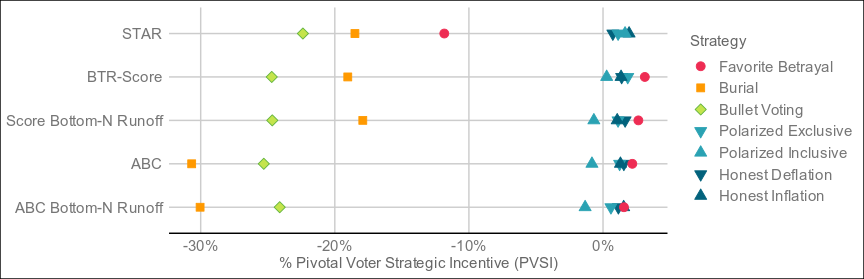
Continued great performance, but may not be worth the increase in complexity.

Below is the code for Bottom-Two and Bottom-N Runoff respectively, with any suggestions for improvement greatly welcome:

        @classmethod
        def results(cls, ballots, **kwargs):
            baseResults = super(BTR0to, cls).results(ballots, **kwargs)
            candidateIndices = list(range(len(baseResults)))
            remainingCandidates = candidateIndices[:]
            while len(remainingCandidates) > 1:
                (secondLowest, lowest) = sorted(remainingCandidates, key=lambda i: baseResults[i])[:2]
                upset = sum(sign(ballot[lowest] - ballot[secondLowest]) for ballot in ballots)
                if upset > 0:
                    remainingCandidates.remove(secondLowest)
                else:
                    remainingCandidates.remove(lowest)
            winner = remainingCandidates[0]
            top = sorted(range(len(baseResults)), key=lambda i: baseResults[i])[-1]
            if winner != top:
                baseResults[winner] = baseResults[top] + 0.01
            return baseResults

    @classmethod
    def results(cls, ballots, **kwargs):
        baseResults = super(BNR0to, cls).results(ballots, **kwargs)
        candidateIndices = list(range(len(baseResults)))
        remainingCandidates = candidateIndices[:]

        def pairwiseLossOrTie(candidate, opponent):
            return sum(sign(ballot[candidate] - ballot[opponent]) for ballot in ballots) <= 0

        def findCondorcetLoser(remainingCandidates):
            for candidate in remainingCandidates:
                if all(pairwiseLossOrTie(candidate, opponent) for opponent in remainingCandidates if opponent != candidate):
                    return candidate
            n = 1
            while len(remainingCandidates) > n:
                for candidate in remainingCandidates:
                    top_n_opponents = sorted(remainingCandidates, key=lambda i: baseResults[i], reverse=True)[:n]
                    if all(pairwiseLossOrTie(candidate, opponent) for opponent in remainingCandidates if opponent not in top_n_opponents):
                        return candidate
                n += 1
            return None

        while len(remainingCandidates) > 1:
            CondorcetLoser = findCondorcetLoser(remainingCandidates)
            if CondorcetLoser is not None:
                remainingCandidates.remove(CondorcetLoser)
        winner = remainingCandidates[0]
        top = sorted(range(len(baseResults)), key=lambda i: baseResults[i])[-1]
        if winner != top:
            baseResults[winner] = baseResults[top] + 0.01
        return baseResults

[Toby Pereira]

@ex-dente-leonem Is Viability-aware just strategic voting? Also how do all the methods do under one-sided strategy? So strategic voting versus honest voting.

[Ex dente leonem]

@toby-pereira said:

@ex-dente-leonem Is Viability-aware just strategic voting?

More or less; each simulated election is preceded by an approval poll which factors into viability-aware strategies.

Also how do all the methods do under one-sided strategy? So strategic voting versus honest voting.

The original vse-sim had one-sided strategy analysis, but the newest version appears to have dropped that in favor of Pivotal Voter Strategic Incentive, which seems to measure how much coordination by one faction it takes to change the outcome. The lower the coordination needed, the greater the PVSI, while near-zero means little strategic effect and negative PVSI indicates greater risk of the strategy backfiring.

[cfrank]

@ex-dente-leonem can you describe the conditions? For example, what is the generic PVSI without a specified strategy? Is it a mean over a bunch of simulations with agents using random strategies?

Also I would like to learn more about agent based modeling and reinforcement learning in this context, I think it could give really interesting results. Finally, how many candidates were there and how were they generated? Probably I’ll have to read the paper.

[Ex dente leonem]

@cfrank said:

@ex-dente-leonem can you describe the conditions? For example, what is the generic PVSI without a specified strategy? Is it a mean over a bunch of simulations with agents using random strategies?

As best as I can tell, the generic PVSI examines (from the point of view of the pivotal voter in a faction which changes the outcome) viability-aware strategies for specific voting methods, which in the case of STAR means:

Balance strategic exaggeration (using 5's and 0's instead of 3's and 2's to maximize influence in the scoring round) with the competing incentive of not wanting to give multiple viable candidates the same score. (This yields more 5's and 0's than the naive strategy and is mostly unaffected by the presence of non-viable candidates in the race.)

while the detailed one looks at the effectiveness of targeted strategies by whichever faction would benefit most from those strategies.

I used the same va-ballots and strategies as STAR for BTR/BNR-Score and ABC, partially because of the similar conflict between maximizing support for preferred candidates while taking later rounds into consideration, but mostly to make as few assumptions and to keep conditions as identical as possible.

Also I would like to learn more about agent based modeling and reinforcement learning in this context, I think it could give really interesting results. Finally, how many candidates were there and how were they generated? Probably I’ll have to read the paper.

Each of the 4000 simulated elections is run with 6 candidates and 101 voters (the difference between 101 and 5001 being minimal) on a hierarchical Dirichlet clustered spatial voter model. I'll run some 3-, 9-, and 12-candidate tests later, and I'm very interested in whether the same performance holds up in other simulations and models.

[cfrank]

@ex-dente-leonem 3x better than what we got so that’s great! Typically how many dimensions are used for candidate platforms in these kinds of simulations?

[Toby Pereira]

@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:

@toby-pereira said:

@ex-dente-leonem Is Viability-aware just strategic voting?

More or less; each simulated election is preceded by an approval poll which factors into viability-aware strategies.

Also how do all the methods do under one-sided strategy? So strategic voting versus honest voting.

The original vse-sim had one-sided strategy analysis, but the newest version appears to have dropped that in favor of Pivotal Voter Strategic Incentive, which seems to measure how much coordination by one faction it takes to change the outcome. The lower the coordination needed, the greater the PVSI, while near-zero means little strategic effect and negative PVSI indicates greater risk of the strategy backfiring.

I see. While also a useful metric, it is different enough for it to be worth having both. As it is we just see the VSE scores and separately this co-ordination measure. But it would be nice to know how much it could drop the VSE by.

[GregW]

@ex-dente-leonem

Ex dente leonem gave these instructions for ABE voting:

Rate each candidate from A to F, A being best and F being worst.

Candidates receive 1 point for each A, B, or C rating and 0 points for each D, E, or F rating.

Equal ratings are allowed. Unrated candidates are automatically rated F.

An explanation for voters:

*The points seed a tournament. The first game matches the candidates with the two lowest point totals.

In each game, the A, B, C, D, E, F ratings determine which candidate is preferred by each voter. If you gave candidate Mike a D, and candidate Tim a B, your vote would go to Tim.

The winner would face the candidate with the next lowest number of points. This is repeated until the survivor meets the candidate with the highest number of points in the final game to determine the winner.

A spoiler effect is nearly impossible with ABC voting.*

ABC is one notch more complex than BTR-Score, which is quite simple as Condorcet methods go.

Is “nearly impossible” a fair statement?

What other benefits should we highlight for the public?

Were you using Jonathan Quinn’s VSE?

Thanks for the great thread.

[Casimir]

I have to admit that I'm confused by the results. I did expect BTR-score to perform well, but I also thought that the difference to Smith//score would be to small to measure. I wonder why there is such a big difference.

Also, when looking at viability-aware, STAR performs a lot better, which is also surprising. Is it that it better utilizes the score part and therefor gets the "best of both worlds"? I don't know.

How long does it take for you to run those simulations?

If it's not too much work, could you try out MARS? It's basically like BTR-score, but each round does not only compare votes, but votes+scores (both measured in % of maximum possible). Previously I thought that that would be even better than BTR-score (on the cost of being complicated), but now I'm no longer sure.

One thing to be cautious of is that these results present very small differences in a high range. It might be that the choice of model has too much of an influence to make decisive claims.

ABC is a good idea and I think could be really a viable method when fleshed out. Most importantly I think there may be more intuitive ways to preset it. Maybe something in between scores and approval, like "ABC-123" where letter ratings count as 0 and numbers as scores.

[Ex dente leonem]

@cfrank Apologies for the late response; most of the voter model is a black box to me but this from the earlier version (in reference to a less complex model):

Voters and candidates each have a location in n-dimensional “ideology space”. A voter’s satisfaction for a given candidate goes down linearly with the ideological distance between the two. Locations are normally distributed, using the same distribution for candidates and voters; and the standard deviations for each dimension follow an exponentially descending sequence such as 1, 1/2, 1/4, 1/8, etc. The number of dimensions is set so as to be large enough that further dimensions would be insignificant. Thus, the only important parameter is the rate of exponential decay; in the example sequence above, it’s 2.

implies it's quite a large number.

[Ex dente leonem]

@toby-pereira I'd like to see that as well. I'll take some time to check out the original CES vse-sim and compare results on both.

[Ex dente leonem]

@gregw said:

A spoiler effect is nearly impossible with ABC voting.*

Is “nearly impossible” a fair statement?

That seems fair, as it requires a cycle of at least four candidates in a specific configuration.

What other benefits should we highlight for the public?

Voters disinclined to vote for the lesser of two evils but also seeking to mitigate their worst outcome can safely do so without actually supporting the less disfavored of two unpopular frontrunners, as expressing preference in ABC doesn't necessitate support, and their full votes can go to more preferred alternatives. I also like that the mechanic is evocative of letter grading and allows voters to rate candidates in a sense similar to what we're already familiar with.

Were you using Jonathan Quinn’s VSE?

Yes, it can be found here.

Thanks for the great thread.

Much appreciated, thank you.

[Ex dente leonem]

@casimir said:

I have to admit that I'm confused by the results. I did expect BTR-score to perform well, but I also thought that the difference to Smith//score would be to small to measure. I wonder why there is such a big difference.

I was wondering the same actually, and I think it may have something to do with how strategic voting is evaluated with Smith methods in vse-sim, specifically existing base methods run on Smith sets. For one thing the only targeted strategy available for analysis by default is bullet voting. I suggest disregarding PVSI and va behavior for Smith//Score and just looking at honest voters, which seem in line with expectations.

Also, when looking at viability-aware, STAR performs a lot better, which is also surprising. Is it that it better utilizes the score part and therefor gets the "best of both worlds"? I don't know.

My speculation is that STAR's single runoff as compared to BTR-Score's several widens the window of advantage for strategy.

How long does it take for you to run those simulations?

It depends on how many moving parts there are, but to give a rough idea here's how many minutes it takes to run 200 elections with 101 voters and 6 candidates on the following methods:

STAR - 1:38
BTR-Score: 1:49
BNR-Score - 2:51
ABC - 1:58
MARS - 1:54 (This one was a pleasant surprise)

But should be a lot faster on newer machines.

One thing to be cautious of is that these results present very small differences in a high range. It might be that the choice of model has too much of an influence to make decisive claims.

Very true, but given that these replicate as closely as possible the conditions of the STAR paper (which is cited as part of official advocacy efforts), I believe they're definitely worthy of attention. That said, these are all excellent methods VSE-wise, and I think most importantly underline how powerful sequential pairwise elimination is as part of any hybrid method,.

If it's not too much work, could you try out MARS? It's basically like BTR-score, but each round does not only compare votes, but votes+scores (both measured in % of maximum possible). Previously I thought that that would be even better than BTR-score (on the cost of being complicated), but now I'm no longer sure.

Have I got great news for you... The title of this thread is officially obsolete.

Here are the result of 4,000 elections:

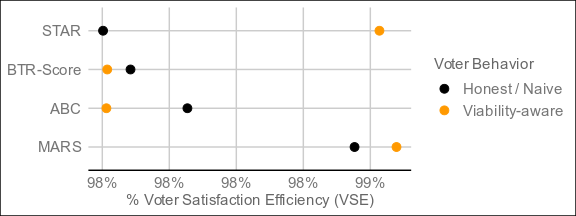
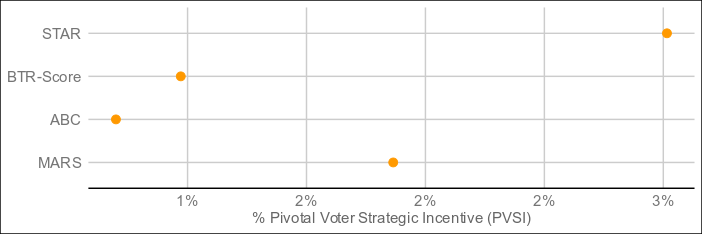
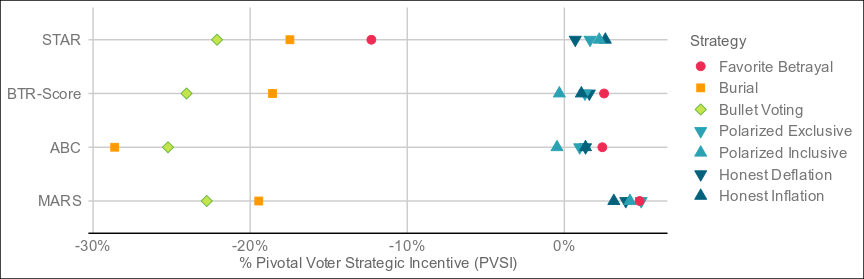
The undisputed best performer by VSE of the four is MARS, which threads the needle between Condorcet and utility methods by being neither and both, and blazing ahead as a result. The resolution mechanism is a step more complex than bottom-two runoff, but still less so than a full pairwise preference matrix (with potentially better results than such), and it resolves in around the same time as ABC and BTR-Score. For electorates who don't care too much about what's under the hood as long as it's transparent, this might be the one.

[Lime]

Thanks for these simulations, they're definitely interesting @Ex-dente-leonem

That said, I think we might be making the mistake of getting sucked deeper and deeper into a drunkard's search. The simulation results here don't really say much, except that we haven't figured out a strategy that breaks Smith//Score or ABC voting yet. That's not surprising, given we only tested 5 of them.

The difficult part of modeling voters isn't showing that one strategy or another doesn't lead to bad results. It's showing that the best possible strategy leads to good results. There's nothing wrong with testing out some strategies like in these simulations, but these are all preliminary findings and can only rule voting methods out, not in.

Just because every integer between 1 and 340 satisfies your conjecture, doesn't mean your conjecture is true. You still need to prove your conjecture.

This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.

The methodology here completely fails to pick up on this, because it only tests pure strategies (i.e. no randomness and everyone plays the same strategy). In practice, pure strategies are rarely, if ever, the best. Ignoring mixed strategies has led the whole field of political science on a 15-year wild goose-chicken-chase that would've been avoided if anyone had taken Game Theory 101.